Number System Questions Practice Question and Answer
8 Q: 64329 को एक निश्चित संख्या से विभाजित किया जाता है। विभाजित करते समय, संख्याएँ, 175, 114 और 213, तीन क्रमागत शेषफलों के रूप में प्रकट होती हैं। भाजक है?
656 06220c43360ee9a48009afe5b
6220c43360ee9a48009afe5b- 1184false
- 2224false
- 3234true
- 4296false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "234 "
Explanation :
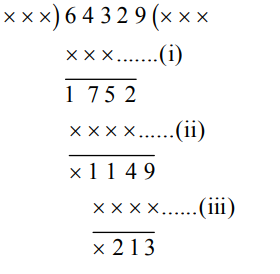
(i) संख्या = 643 – 175 = 468
(ii) संख्या = 1752 – 114 = 1638
(iii) संख्या = 1149 – 213 = 936
स्पष्टतः, 468, 1638 और 936, 234 और 234 > 213 के गुणज हैं।
भाजक = 234
Q: एक संख्या 13 से विभाजित करने पर शेषफल 1 आता है और भागफल को 5 से विभाजित करने पर शेषफल 3 आता है यदि उसी संख्या को 65 से विभाजित किया जाएतो शेषफल क्या होगा
1129 05d7f1ae6fb24f902086364bb
5d7f1ae6fb24f902086364bb- 128false
- 216false
- 318false
- 440true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "40"
Explanation :
माना सबसे छोटी संख्या x है
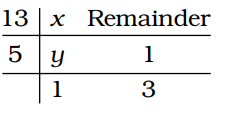
y = 5 × 1 + 3 = 8
x = 13 × 8 + 1 = 105
105 को 65 से विभाजित करने पर शेषफल = 40
Q: एक संख्या को जब 6 से विभाजित किया जाता है तो शेषफल 3 बचता है। जब उसी संख्या के वर्ग को 6 से विभाजित किया जाता है, तो शेषफल होता है:
379 0650d36e3d2f211504875ecda
650d36e3d2f211504875ecda- 10false
- 21false
- 32false
- 43true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "3"
Explanation :
शेष वही रहेगा.
9 को 6 से विभाजित करने पर शेषफल = 3
81 को 6 से विभाजित करने पर शेषफल = 3
Q: जब एक संख्या को 119 से विभाजित किया जाता है, तो 19 शेष रहता है । यदि इसी संख्या को 17 से विभाजित किया जाए तो शेष होगा –
819 0614c68834d59797c590e504e
614c68834d59797c590e504e- 119false
- 27false
- 310false
- 42true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "2 "
Explanation :
दी गई संख्या को 119 से विभाजित करने पर, मान लीजिए कि भागफल k है और शेषफल 19 है।
तो, संख्या = 119k + 19
= 17 × 7k + 17 × 1 + 2
= 17 (7k + 1) + 2
इसलिए, दी गई संख्या को 17 से विभाजित करने पर भागफल (7k + 1) और शेषफल 2 मिलता है।
Q: 3 और 200 के बीच 7 से विभाजित होने वाली कितनी प्राकृतिक संख्यायें होगी?
960 05ee845d3a08a50198d8d094c
5ee845d3a08a50198d8d094c- 128true
- 229false
- 327false
- 436false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "28 "
Explanation :
3 से थोड़ी बड़ी संख्या जो 7 से विभाज्य है = 7
200 से थोड़ी छोटी संख्या जो 7 से विभाज्य है = 196
यहाँ, a = 7, an = 196,
d = 7, n = 8
an = a + (n –1)d
⇒196 = 7 + (n – 1) × 7
⇒ 
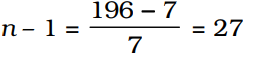
⇒ n = 27 + 1 = 28
Note : We can find the answer after dividing 200 by 7. The quotient is your answer.
Q: पिकनिक पार्टी के प्रत्येक सदस्य ने दो बार योगदान दिया और कुल संग्रह में 3042 रुपये का योगदान था। पार्टी में उपस्थित सदस्यों की संख्या थी
921 05ec4a257980ff60a66c06591
5ec4a257980ff60a66c06591- 12false
- 232false
- 342false
- 439true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "39"
Explanation :
माना व्यक्तियों की आवश्यक संख्या x है।
प्रश्न के अनुसार, 2x2 = 3042
या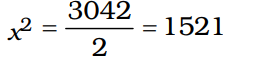 
या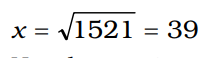 
Q: किसी संख्या को 296 से भाग देने पर शेषफल 75 प्राप्त होता है यदि उसी संख्या को 37 से भाग दिया जाये , तो शेषफल प्राप्त होगा ।
883 05ee8426479b5ea388bec0116
5ee8426479b5ea388bec0116- 18false
- 21true
- 32false
- 411false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "1 "
Explanation :
माना संख्या (लाभांश) X है।
∴ X = 296 × Q + 75 जहां Q भागफल है और इसके मान 1, 2, 3 आदि हो सकते हैं।
= 37 × 8 × Q + 37 × 2 + 1
= 37 (8Q + 2) + 1
इस प्रकार हम देखते हैं कि शेषफल 1 है।
[टिप्पणी: जब दूसरा भाजक पहले भाजक का एक गुणनखंड हो, तो पहले शेषफल को दूसरे भाजक से विभाजित करने पर दूसरा शेषफल प्राप्त होता है।
अतः, 75 को 37 से विभाजित करें, शेषफल 1 है]।
Q: जब 1062, 1134 और 1182 को सबसे बड़ी संख्या .x से विभाजित किया जाता है, तो प्रत्येक स्थिति में शेषफल y होता है। (x − y) का मान क्या है?
399 064ba4fa5c3da05b2213e134d
64ba4fa5c3da05b2213e134d- 117false
- 218true
- 316false
- 419false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "18"
Explanation :
