SSC और बैंक पीओ के उदाहरणों के साथ प्रोबेबिलिटी फॉर्मूला

प्रतियोगी परीक्षाओं में प्रोबेबिलिटी प्रश्नों को हल करने के लिए अधिकांश छात्रों को सूत्रों का उपयोग करने में समस्या का सामना करना पड़ता है। वे केवल इस बारे में सोचते हैं कि वे प्रोबेबिलिटी सूत्रों का सही उपयोग कैसे कर सकते हैं। यदि आपको भी इससे संबंधित प्रश्नों को हल करने में समस्या होती हैं, तो आप यहाँ उदाहरणों के साथ प्रोबेबिलिटी सूत्रों का सही उपयोग करना सीख सकते हैं।
इस ब्लॉग में आप प्रोबेबिलिटी समस्याओं के सूत्र आसानी से प्राप्त कर सकते हैं। आप प्रोबेबिलिटी प्रश्नों और उत्तरों का अभ्यास करने के साथ-साथ उदाहरणों के साथ प्रोबेबिलिटी फॉर्मूला के उपयोग को भी सीख सकते हैं।
प्रतियोगी परीक्षाओं के उदाहरण के साथ प्रोबेबिलिटी फॉर्मूला
1. एक्सपेरिमेंट: एक ऑपरेशन जो कुछ अच्छी तरह से परिभाषित परिणाम उत्पन्न कर सकता है उसे प्रयोग कहा जाता है।
2. रेंडम एक्सपेरिमेंट: एक प्रयोग जिसमें सभी संभावित परिणाम ज्ञात होते हैं और सटीक आउटपुट का पहले से अनुमान नहीं लगाया जा सकता है, एक यादृच्छिक प्रयोग कहलाता है।
रेंडम एक्सपेरिमेंट प्रयोग करने के उदाहरण:
(A) एक निष्पक्ष पासा रोलिंग।
(B) एक निष्पक्ष सिक्का उछालना।
(C) अच्छी तरह से फेंटे गए कार्डों के पैक से एक कार्ड खींचना
(D) विभिन्न रंगों की गेंदों वाले बैग से एक निश्चित रंग की गेंद को उठाना।
विवरण:
(A) जब हम एक सिक्का फेंकते हैं। फिर या तो एक हेड (H) या टेल (T) दिखाई देता है।
(B) एक पासा एक ठोस घन है, जिसमें 6 बर्फ क्रमशः 1, 2, 3, 4, 5, 6 चिह्नित हैं।
जब एक पासे को फेंका जाता है, तो परिणाम उसके ऊपरी फलक पर दिखाई देने वाली संख्या होती है।
(C) कार्ड के एक पैक में 52 कार्ड हैं।
इसमें प्रत्येक सूट के 13 कार्ड हैं, जैसे हुकुम, क्लब, दिल और हीरे।
हुकुम और क्लब के कार्ड ब्लैक कार्ड हैं।
प्रत्येक सूट के 4 सम्मान हैं
ये इक्के, राजा, क्वींस और जैक हैं।
इन्हें फेस कार्ड कहा जाता है।
3. सेंपल स्पेस: जब हम कोई प्रयोग करते हैं, तो सभी संभावित परिणामों के समुच्चय S को प्रतिदर्श समष्टि कहते हैं।
सेंपल स्पेस के उदाहरण:
(i) एक सिक्के को उछालने में = S = {H, T}
(ii) यदि दो विपक्षों को उछाला जाता है, तो S = {HH, HT, TH, TT}।
(iii) एक पासे को पलटने में, S = [1,2,3,4,5,6] प्राप्त होता है।
4. घटना: सेंपल स्पेस के किसी उपसमुच्चय को घटना कहते हैं।
5. किसी घटना के घटित होने की प्रायिकता:
मान लीजिए S सेंपल स्पेस है और E एक घटना है।
फिर, E⊆S.
6. प्रोबेबिलिटी पर परिणाम:
(i) P (S) = 1 (ii) 0≤P (E) ≤ 1. (iii) P (⏀) = 0
(iv) किसी भी घटना A और B के लिए, हमारे पास है:
P (A ∪ B) = P(A) + P(B) – P ( A ∩ B)
(v) यदि 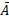 का अर्थ है (not-A), फिर P (
का अर्थ है (not-A), फिर P (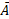 ) = 1 – P (A).
) = 1 – P (A).
उदाहरण
Ex.1. एक सिक्के को फेंकने में, एक चित आने की प्रोबेबिलिटी ज्ञात कीजिए।
व्याख्या
यदि S = {H, T} और E = {H}
Ex.2. दो निष्पक्ष सिक्के उछाले जाते हैं। अधिकतम एक हेड आने की प्रोबेबिलिटी क्या है ?
व्याख्या
यहां S = {HH, TH, TT}.
मान लीजिए E = अधिकतम एक हेड मिलने की घटना।
∴ E = {TT, HT, TH}.
Ex.3. एक निष्पक्ष पासा फेंका जाता है। 3 का गुणा प्राप्त करने की प्रोबेबिलिटी ज्ञात कीजिए।
व्याख्या
यहां S = {1,2,3,4,5,6}
मान लीजिए कि E 3 का गुणा प्राप्त करने की घटना है।
फिर, E = {3,6}
Ex.4. पासों के एक जोड़े को एक साथ फेंकने पर, कुल 7 से अधिक प्राप्त करने की प्रोबेबिलिटी ज्ञात कीजिए।
व्याख्या
यहां , n (S) = (6×6) = 36.
मान लीजिए E = कुल 7 से अधिक प्राप्त करने की घटना।
= {(2,6), (3,5),(3,6),(4,4), (4,5), (4,6), (5,3), (5,4), (5,5), (5,6), (6,2), (6,3), (6,4), (6,5), (6,6)}
Ex.5. दो पासे एक साथ फेंके जाते हैं। क्या प्रोबेबिलिटी है कि दोनों फलकों पर संख्याओं का योग 4 या 6 से विभाज्य है?
व्याख्या
स्पष्ट रूप से, n (S) = 6×6=36.
मान लीजिए कि दो फलकों पर संख्याओं का योग 4 या 6 से विभाज्य है, तो E घटना है
E = { (1,3), (1,5), (2,2), (2,4), (2,6), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (6,2), (6,6)}
∴ n(E) = 14.
मुझे आशा है कि ये सूत्र आपके लिए सहायक होंगे। यदि आपको कोई समस्या और संदेह है या आप मुझसे उदाहरण के साथ संभाव्यता सूत्रों के बारे में कुछ पूछना चाहते हैं, तो आप मुझसे कमेंट बॉक्स में पूछ सकते हैं।
ऑल द बेस्ट।



