संख्या प्रणाली प्रश्न और समाधान उत्तर सहित

विभाजन के किसी प्रश्न में भाजक, भागफल का 4 गुना है तथा शेषफल का 3 गुना है । यदि शेषफल 4 है, तो भाज्य हैं।
(A) 36
(B) 40
(C) 12
(D) 30
Correct Answer : B
Explanation :
शेष =4
⇒ भाजक = 3 × 4 = 12
पुनः, भाजक = 4 × भागफल
⇒ 4 × भागफल = 12
भागफल =
⇒ लाभांश = 3 × 12 + 4 = 40
पिकनिक पार्टी के प्रत्येक सदस्य ने दो बार योगदान दिया और कुल संग्रह में 3042 रुपये का योगदान था। पार्टी में उपस्थित सदस्यों की संख्या थी
(A) 2
(B) 32
(C) 42
(D) 39
Correct Answer : D
Explanation :
माना व्यक्तियों की आवश्यक संख्या x है।
प्रश्न के अनुसार, 2x2 = 3042
या 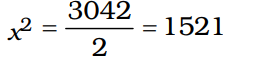
या 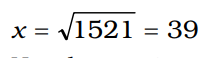
3 और 200 के बीच 7 से विभाजित होने वाली कितनी प्राकृतिक संख्यायें होगी?
(A) 28
(B) 29
(C) 27
(D) 36
Correct Answer : A
Explanation :
3 से थोड़ी बड़ी संख्या जो 7 से विभाज्य है = 7
200 से थोड़ी छोटी संख्या जो 7 से विभाज्य है = 196
यहाँ, a = 7, an = 196,
d = 7, n = 8
an = a + (n –1)d
⇒196 = 7 + (n – 1) × 7
⇒ 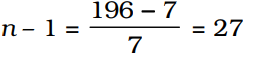
⇒ n = 27 + 1 = 28
Note : We can find the answer after dividing 200 by 7. The quotient is your answer.
1 से लेकर 60 तक की सभी संख्याओं का योग निम्न में से किससे विभाजित होगा ।
(A) 13
(B) 60
(C) 61
(D) 59
Correct Answer : C
Explanation :
प्रथम 60 संख्याओं का योग
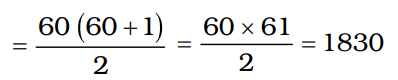
संख्या 1830, 61 से विभाज्य है।
एक संख्या को जब 3 से विभाजित किया जाता है तो शेषफल 1 रहता है। जब भागफल को 2 से विभाजित किया जाता है, तो शेषफल 1 रहता है। संख्या को 6 से विभाजित करने पर शेषफल क्या होगा?
(A) 5
(B) 2
(C) 3
(D) 4
Correct Answer : D
Explanation :
सबसे छोटी संख्या (लाभांश) x इस प्रकार प्राप्त होती है:
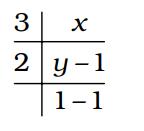
y = 2 × 1 + 1 = 3
x = 3 × 3 + 1 = 10
जब हम 10 को 6 से विभाजित करते हैं, तो शेषफल = 4 होता है
दो संख्याओं का गुणनफल 9375 है। जब बड़ी संख्या को छोटी संख्या से विभाजित किया जाता है तो, भागफल 15 आता है। संख्याओं का योग ज्ञात करे ?
(A) 395
(B) 380
(C) 400
(D) 425
Correct Answer : C
Explanation :
माना संख्याएँ x और y हैं और x, y से बड़ा है।
जैसा कि दिया गया है,
xy = 9375 ....(i)
दोबारा,
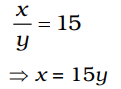
∴ समीकरण (i) से,
15y × y = 9375
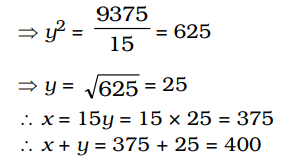
जब एक संख्या को 119 से विभाजित किया जाता है, तो 19 शेष रहता है । यदि इसी संख्या को 17 से विभाजित किया जाए तो शेष होगा –
(A) 19
(B) 7
(C) 10
(D) 2
Correct Answer : D
Explanation :
दी गई संख्या को 119 से विभाजित करने पर, मान लीजिए कि भागफल k है और शेषफल 19 है।
तो, संख्या = 119k + 19
= 17 × 7k + 17 × 1 + 2
= 17 (7k + 1) + 2
इसलिए, दी गई संख्या को 17 से विभाजित करने पर भागफल (7k + 1) और शेषफल 2 मिलता है।
(719 + 2) को 6 से भाग देने पर शेषफल होगा :
(A) 2
(B) 1
(C) 5
(D) 3
Correct Answer : D
Explanation :
द्विपद विस्तार से हमारे पास है
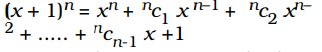
यहां, अंतिम पद को छोड़कर प्रत्येक पद में x शामिल है। जाहिर है, अंतिम पद को छोड़कर प्रत्येक पद x से पूर्णतः विभाज्य है।
उसी तर्क का पालन करते हुए,
719 = (6 + 1)19 में अंतिम पद को छोड़कर प्रत्येक पद 6 से विभाज्य है।
अतः, 719 + 2 को 6 से विभाजित करने पर शेषफल =1 + 2 = 3 बचता है
जब एक संख्या को 357 से विभाजित किया जाता है तो शेष 39 प्राप्त होता है। यदि उस संख्या को 17 से विभाजित किया जाता है, तो शेषफल होगा:
(A) 5
(B) 11
(C) 0
(D) 3
Correct Answer : A
Explanation :
यहाँ, 357, 17 से पूर्णतः विभाज्य है।
∴ आवश्यक शेषफल = 39 को 17 से विभाजित करने पर प्राप्त शेषफल = 5
एक संख्या को 68 से विभाजित करने पर भागफल 269 और शेषफल शून्य प्राप्त होता है। यदि उसी संख्या को 67 से विभाजित किया जाता है, तो शेषफल होता है:
(A) 2
(B) 3
(C) 0
(D) 1
Correct Answer : D
Explanation :
संख्या = 269 × 68
= 269 × (67 + 1)
= 269 × 67 + 269
स्पष्टतः, 269 को 67 से विभाजित करने पर शेषफल 1 प्राप्त होता है



