Maths Practice Question and Answer
8 Q: निम्नलिखित में से कौन सा भिन्न सबसे छोटा है?
574 065081b75e918d9427f49639d
65081b75e918d9427f49639d- 1false
- 2false
- 3false
- 4true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "
Explanation :

Q: एक संख्या को 192 से विभाजित करने पर शेषफल 54 प्राप्त होता है। उसी संख्या को 16 से विभाजित करने पर क्या शेषफल प्राप्त होगा?
782 0650d458363078e50a2943253
650d458363078e50a2943253- 12false
- 24false
- 36true
- 48false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "6"
Explanation :
Here, the first divisor 192 is a multiple of second divisor 16.
∴ Required remainder
= remainder obtained by dividing 54 by 16 = 6
Q: एक संख्या को 5 से विभाजित करने पर शेषफल 3 बचता है। जब उसी संख्या के वर्ग को 5 से विभाजित करने पर शेषफल क्या बचता है?
742 0650d43a2cb11fc5036d68479
650d43a2cb11fc5036d68479- 11false
- 22false
- 33false
- 44true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "4"
Q: एक संख्या दो अंकों से बनी होती है। यदि अंकों को आपस में बदलने से बनी संख्या को मूल संख्या में जोड़ दिया जाए, तो परिणामी संख्या (अर्थात योग) विभाज्य होनी चाहिए
665 0650d423410a18f5082eccafc
650d423410a18f5082eccafc- 111true
- 29false
- 35false
- 43false
- Show Answer
- Workspace
- SingleChoice
Answer : 1. "11"
Explanation :
माना संख्या 10x + y है
अंकों को आपस में बदलने के बाद,
प्राप्त संख्या = 10y + x
प्रश्न के अनुसार,
परिणामी संख्या
= 10x + y + 10y + x
= 11x + 11y
= 11 (x + y)
जो कि 11 से पूर्णतः विभाज्य है।
Q: यदि दो संख्याओं को एक ही भाजक से विभाजित किया जाए, तो शेषफल क्रमशः 3 और 4 होता है। यदि दो संख्याओं के योग को एक ही भाजक से विभाजित किया जाए, तो शेषफल 2 होता है। भाजक है
775 0650d401473357650645d2108
650d401473357650645d2108- 19false
- 27false
- 35true
- 43false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "5 "
Explanation :
आवश्यक भाजक = 3 + 4 – 2 = 5
Q: भाग के एक प्रश्न में भाजक भागफल का 7 गुना और शेषफल का 3 गुना है। यदि शेषफल 28 है, तो लाभांश है
618 0650d3f3f73357650645d20e3
650d3f3f73357650645d20e3- 1588false
- 2784false
- 3823false
- 41036true
- Show Answer
- Workspace
- SingleChoice
Answer : 4. "1036"
Explanation :
माना कि भागफल Q है और शेषफल R है
भाजक = 7 Q = 3 R
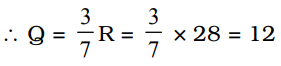
∴ भाजक = 7 Q = 7 × 12 = 84
लाभांश = भाजक × भागफल + शेषफल = 84 × 12 + 28 = 1008 + 28 = 1036
Q: 64329 को जब किसी संख्या से भाग दिया जाता है, तो 175, 114 तथा 213 लगातार तीन शेषफल आते है, तो भाज्य है?
1895 05d91f524a01ffd5718894157
5d91f524a01ffd5718894157- 1184false
- 2224false
- 3234true
- 4296false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "234"
Explanation :
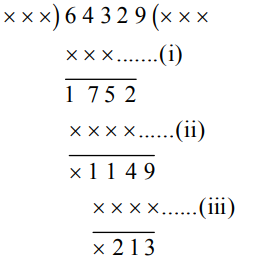
(i) संख्या = 643 – 175 = 468
(ii) संख्या = 1752 – 114 = 1638
(iii) संख्या = 1149 – 213 = 936
स्पष्टतः, 468, 1638 और 936, 234 और 234 > 213 के गुणज हैं।
भाजक = 234
Q: 64329 को एक निश्चित संख्या से विभाजित किया जाता है। विभाजित करते समय, संख्याएँ, 175, 114 और 213, तीन क्रमागत शेषफलों के रूप में प्रकट होती हैं। भाजक है?
813 06220c43360ee9a48009afe5b
6220c43360ee9a48009afe5b- 1184false
- 2224false
- 3234true
- 4296false
- Show Answer
- Workspace
- SingleChoice
Answer : 3. "234 "
Explanation :
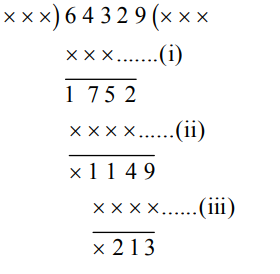
(i) संख्या = 643 – 175 = 468
(ii) संख्या = 1752 – 114 = 1638
(iii) संख्या = 1149 – 213 = 936
स्पष्टतः, 468, 1638 और 936, 234 और 234 > 213 के गुणज हैं।
भाजक = 234

