SSC और बैंक परीक्षाओं के उदाहरणों के साथ नाव और धारा सूत्र

अक्सर छात्रों को प्रतियोगी परीक्षा के प्रश्नों में नावों और धाराओं के सूत्रों का उपयोग करने में कठिनाई का सामना करना पड़ता है क्योंकि वे नावों और धाराओं के प्रश्नों या समीकरणों को हल करने का उचित तरीका नहीं जानते हैं। ये नावों और धारा प्रश्न आमतौर पर एसएससी और बैंक परीक्षाओं में पूछे जाते हैं।
तो यहाँ इस ब्लॉग में, आप प्रतियोगी परीक्षाओं के उदाहरणों के साथ बोट और स्ट्रीम फ़ार्मुलों का उपयोग करना सीखने के लिए अपने प्रदर्शन में सुधार कर सकते हैं। आप अपनी प्रतियोगी परीक्षाओं में बेहतर अंक प्राप्त करने के लिए इन उत्तरों के साथनावों और धाराओं प्रश्नों का अभ्यास भी कर सकते हैं और उत्तरों के साथ प्रश्नों को स्ट्रीम कर सकते हैं।
प्रतियोगी परीक्षाओं में समय पर प्रश्नों को पूरा करने के लिए पर्याप्त उदाहरणों के साथ नावों और धाराओं की समस्याओं को हल करने के लिए यहां क्लिक करें।
प्रतियोगी परीक्षाओं के उदाहरणों के साथ नाव और धारा के सूत्र
डाउनस्ट्रीम मूवमेंट
जब एक नदी और नाव की गति की दिशा समान होती है, तो उनकी सामूहिक गति को अनुप्रवाह गति के रूप में जाना जाता है। और नाव द्वारा तय की गई दूरी को अनुप्रवाह दूरी के रूप में जाना जाता है।
यदि शांत जल में नाव की गति x है और धारा की गति y है, तो धारा के अनुकूल गति = x+y
अप-स्ट्रीम मूवमेंट
जब नदी और नाव की गति की दिशा विपरीत होती है, तो उन्हें धारा के विपरीत गति में कहा जाता है। इस मामले में तय की गई दूरी को अपस्ट्रीम दूरी के रूप में जाना जाता है।
यदि नदी की गति = x और नाव की गति = y, तो धारा के प्रतिकूल गति = x-y
महत्वपूर्ण तथ्य -
1. स्थिर जल का अर्थ है कि नदी में जल की गति शून्य है।
2. धारा के पानी का अर्थ है कि नदी में पानी चल रहा है।
3. यदि एक शांत जल की गति x है और धारा की गति y है, तो
* अनुप्रवाह की गति = x + y
* अपस्ट्रीम की गति =x-y
* शांत पानी में नाव की गति(x)=1/2 (डाउनस्ट्रीम की गति + धारा के ऊपर गति)
* धारा की गति (y) = 1/2(गति के अनुप्रवाह - गति ऊपर धारा)
महत्वपूर्ण सूत्र -
1. यदि शांत जल में नाव की गति u किमी/घंटा है और धारा की गति v किमी/घंटा है, तो:
अनुप्रवाह की गति = (u+v) किमी/घंटा।
धारा के प्रतिकूल गति = (u-v) किमी/घंटा।
2. यदि अनुप्रवाह की गति एक किमी/घंटा है और धारा के प्रतिकूल गति b किमी/घंटा है, तो:
शांत जल में गति = 1/2 (a+b) किमी/घंटा।
धारा की दर = 1/2 (a+b) किमी/घंटा।
हल किया गया उदाहरण
Ex.1. एक आदमी धारा के प्रतिकूल 7 किमी प्रति घंटे की रफ्तार से और धारा के अनुकूल 10 किमी प्रति घंटे की रफ्तार से नाव चला सकता है। शांत जल में मनुष्य की दर और धारा की दर ज्ञात कीजिए।
Solution:
स्थिर पानी में दर = 1/2(10+7) km/hr = 8.5
वर्तमान की दर = 1/2(10-7) km/hr = 1.5 km/hr.
Ex.2. एक व्यक्ति नदी के अनुप्रवाह में 15 किमी नाव चलाने में 3 घंटे 45 मिनट और धारा के प्रतिकूल 5 किमी की दूरी तय करने में 2 घंटे 30 मिनट का समय लेता है। किमी/घंटा में नदी की धारा का व्यय ज्ञात कीजिए।
Solution:
दर नीचे की ओर = 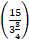 km/hr =
km/hr = 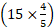 km/hr = 4 km/hr.
km/hr = 4 km/hr.
दर ऊपर की ओर = 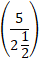 km/hr =
km/hr = ![]() km/hr = 2 km/hr.
km/hr = 2 km/hr.
∴धारा की गति =  (4-2) km/hr = 1 km/hr.
(4-2) km/hr = 1 km/hr.
Ex.3. एक आदमी शांत पानी में 18 किमी प्रति घंटे की रफ्तार से दौड़ सकता है। उसे नदी के नीचे पंक्तिबद्ध करने में तीन गुना अधिक समय लगता है। धारा की दर ज्ञात कीजिए।
Solution:
मान लीजिए मनुष्य की धारा के प्रतिकूल गति x किमी/घंटा है। फिर, उसकी दर नीचे की ओर = 3x kmph
∴स्थिर पानी में दर =  (3x+x) kmph = 2x kmph.
(3x+x) kmph = 2x kmph.
तो, 2x = 18 or x = 9.
∴ दर ऊपर की ओर = 9 km/hr, दर नीचे की ओर=27 km/hr.
इसलिए दर =  (27-9) km/hr = 9 km/hr.
(27-9) km/hr = 9 km/hr.
Ex.4. नदी के किनारे एक सड़क है। दो मित्र एक स्थान A से चलना शुरू करते हैं, दूसरे स्थान B पर स्थित मंदिर में चले जाते हैं और फिर A में वापस लौट आते हैं। उनमें से एक साइकिल पर 12 किमी/घंटा की गति से चलता है, जबकि दूसरा नाव पर 10 किमी/घंटा की गति से चलता है। यदि नदी 4 किमी/घंटा की गति से बहती है, तो दोनों में से कौन मित्र पहले स्थान पर लौटेगा?
Solution:
स्पष्ट है कि साइकिल चालक दोनों ओर 12 किमी/घंटा की गति से चलता है।
तो, साइकिल चालक की औसत गति = 12 km/hr.
नाव नाविक नीचे की ओर @ (10+4) चलता है अर्थात, 14 km/hr and ऊपर की ओर@ (10-4) i.e, 6 km/hr.
So, average speed of the boat sailor
Ex.5. एक आदमी शांत पानी में 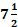 किमी प्रति घंटे की रफ्तार से दौड़ सकता है। अगर 1.5 किमी प्रति घंटे की रफ्तार से चलने वाली नदी में। उसे एक स्थान तक जाने और वापस जाने में 50 मिनट लगते हैं, वह स्थान कितनी दूर है?
किमी प्रति घंटे की रफ्तार से दौड़ सकता है। अगर 1.5 किमी प्रति घंटे की रफ्तार से चलने वाली नदी में। उसे एक स्थान तक जाने और वापस जाने में 50 मिनट लगते हैं, वह स्थान कितनी दूर है?
Solution:
गति नीचे की ओर = (7.5+1.5) kmph = 9kmph;
गति ऊपर की ओर = (7.5 – 1.5) kmph = 6 kmph,
माना कि अभीष्ट दूरी x किमी है। फिर,
अत: अभीष्ट दूरी 3 km है।
आप इन सूत्रों की सहायता से नावों और जलधाराओं की समस्याओं का अभ्यास कर सकते हैं। यदि आपको कोई शंका या समस्या है तो आप मुझसे ssc और बैंक परीक्षाओं के उदाहरणों के साथ नावों और धाराओं के फॉर्मूले के बारे में कुछ भी पूछ सकते हैं।



