प्रतियोगी परीक्षाओं के लिए पाइप और सिस्टर्न की समस्या

पाइप्स एंड सिस्टर्न प्रॉब्लम्स एप्टीट्यूड सेक्शन का हिस्सा हैं। इन समस्याओं में छात्रों को स्थिति या कथन के अनुसार सही उत्तर खोजने होते हैं। पाइप्स और सिस्टर्न की समस्याओं को हल करना मुश्किल नहीं है, आपको इसे हल करने के लिए केवल समस्या को समझने की जरूरत है।
आपकी बेहतर तैयारी के लिए, यहां मैं आपको पाइप्स एंड सिस्टर्न प्रॉब्लम्स विद सॉल्यूशंस दे रहा हूं जो आपको इस विषय के साथ-साथ इसकी समस्याओं को समझने में मदद करता है। आप यह जान सकते हैं कि हल करते समय पाइप्स और सिस्टर्न की समस्याओं में सूत्रों का उपयोग कैसे किया जाता है।
समाधान के साथ पाइप और सिस्टर्न की समस्याएं
Q.1. दो पाइप A और B अलग-अलग एक हौज को क्रमश: 60 मिनट और 75 मिनट में भर सकते हैं। इसे खाली करने के लिए टंकी के तल में एक तीसरा पाइप है। यदि सभी ट्री पाइपों को एक साथ खोल दिया जाए, तो टंकी 50 मिनट में भर जाती है। तीसरा पाइप अकेले टंकी को कितने समय में खाली कर सकता है?
(A) 80 min
(B) 100 min
(C) 110 min
(D) 120 min
Ans . B
तीसरे पाइप द्वारा 1 मिनट में किया गया कार्य।
$$ = {1\over 50}- \left( {1\over60}+{1\over 75} \right)= \left( {1\over 50}-{3\over 100} \right)= -{1\over 100} [ - \ ve \ sign \ means \ emptying] $$
∴ तीसरा पाइप अकेला खाली टंकी को 100 मिनट में खाली कर सकता है।
Q.2. एक टंकी को एक नल 4 घंटे में भर सकता है जबकि दूसरा नल इसे 9 घंटे में खाली कर सकता है। यदि दोनों नलों को एक साथ खोल दिया जाए तो कितने समय बाद टंकी भर जाएगी?
(A) 4.5 hrs
(B) 5 hrs
(C) 6.5 hrs
(D) 7.2 hrs
Ans . D
1 घंटे में भर गया शुद्ध भाग = $$ \left( {1\over 4}-{1\over 9}= {5\over 36} \right). $$
⸫ टंकी
Q.3. एक पंप एक टंकी को 2 घंटे में पानी से भर सकता है। टंकी में रिसाव होने के कारण टंकी को भरने में 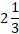 घंटे का समय लगा। रिसाव से टैंक का सारा पानी निकल सकता है:
घंटे का समय लगा। रिसाव से टैंक का सारा पानी निकल सकता है:
(A) ![]() hrs
hrs
(B) 8 hrs
(C) 10 hrs
(D) 14 hrs
Ans . D
1 घंटे में लीक से किया काम = $$ \left( {1\over 2} - {3\over 7} \right)= {1\over 14} $$
∴ लीक 14 घंटे में टैंक को खाली कर देगा।
Q.4. एक नल एक टंकी को 6 घंटे में भर सकता है। टंकी भर जाने के बाद, तीन और समान नल खोले जाते हैं। टैंक को पूरी तरह से भरने में लिया गया कुल समय कितना है?
(A) 3 hrs
(B) 3 hrs 45 min
(C) 4 hrs
(D) 5 hrs 15.
Ans . B
आधा टैंक भरने के लिए एक नल द्वारा लिया गया समय और समय = 3 hrs.
1 घंटे में चार नलों से भरा भाग = $$ \left( 4 × {1\over 6} \right)= {2\over 3}. $$
शेष भाग = $$ \left( 1 - {1\over 2} \right)= {1\over 2} $$
$$ ∴ {2\over 3}: {1\over 2}:: 1: x \ or\ x= \left( {1\over2}×1×{3\over 2} \right)= {3\over 4} \ hrs \ i.e, \ 45 \ mins $$
Q.5. एक पाइप एक टैंक को दूसरे पाइप की तुलना में तीन गुना तेजी से भर सकता है। यदि दोनों पाइप मिलकर 36 मिनट में टैंक को भर सकते हैं, तो धीमा पाइप अकेले टैंक को भरने में सक्षम होगा:
(A) 80 min
(B) 108 min
(C) 144 min
(D 180 min
Ans . C
मान लीजिए कि धीमा पाइप अकेले टैंक को x मिनट में भरता है।
फिर, तेज़ पाइप इसे
⸫ $$ {1\over x}+{3\over x}= {1\over 36} $$
$$ ⟺ {4\over x} = {1\over 36} ⟺ x=144 min $$
Q.6. एक पानी की टंकी दो-पांचवीं भरी होती है। पाइप A एक टैंक को 10 मिनट में भर सकता है और पाइप B इसे 6 मिनट में खाली कर सकता है। यदि दोनों पाइप खुले हैं, तो टैंक को खाली करने या पूरी तरह से भरने में कितना समय लगेगा?
(A) 6 min to empty
(B) 6 min to fill
(C) 8min to empty
(D) 8 min to fill
(E) None of these
Ans . A
स्पष्ट है, पाइप B, पाइप A से तेज है और इसलिए, टैंक खाली हो जाएगा।
खाली किया जाने वाला भाग =
 .
.Part emptied by (A+B) in 1 minute $$= \left( {1\over 6}-{1\over10} \right)= {1\over 15} $$
$$∴ {1\over 15}: {2\over 5}::1:x \ or \ x = \left({2\over5}×1×{15} \right)=6 \ min. $$
अत: टंकी 6 मिनट में खाली हो जाएगी।
Q.7. एक टैंक को तीन पाइप A, B और C द्वारा 5 घंटे में भर दिया जाता है। पाइप C, B से दोगुना तेज है और B, A से दोगुना तेज है। पाइप A अकेले टैंक को भरने में कितना समय लेगा?
(A) 15 hrs
(B) 25 hrs
(C) 35 hrs
(D)45
(E) इनमे से कोई नहीं
Ans . C
मान लीजिए कि पाइप A अकेले टैंक को भरने में x घंटे लेता है।
फिर, पाइप B और C को टैंक को भरने में क्रमशः
$$ {1\over x}+{2\over x}+{4\over x}={1\over 5}$$
$$⟺ {7\over x}= {1\over 5}⟺ x = 35 \ hrs $$
Q.8. पाइप A एक टैंक को 5 घंटे में, पाइप B 10 घंटे में और पाइप C 30 घंटे में भर सकता है। यदि सभी पाइप खुले हैं, तो टंकी कितने घंटे में भर जाएगी?
(A) 1
(B) 2.5
(C) 3
(D) 3.5
Ans . C
1 घंटे में (A+B+C) द्वारा भरा गया भाग = $$ \left( {1\over 5}+{1\over 10}+{1\over 30} \right)= {1\over 3} $$∴ तीनों पाइप मिलकर टंकी को 3 घंटे में भरेंगे.
Q.9. एक टैंक को एकसमान प्रवाह वाले तीन पाइपों से भरा जाता है। एक साथ काम करने वाले पहले दो पाइप टैंक को उतने ही समय में भरते हैं, जितने समय में टैंक को तीसरा पाइप अकेला भरता है। दूसरा पाइप टैंक को पहले पाइप से 5 घंटे तेज और तीसरे पाइप से 4 घंटे धीमी गति से भरता है। पहले पाइप के लिए आवश्यक समय है:
(A) 6 hrs
(B) 12 hrs
(C) 15 hrs
(D) 30 hrs
Ans . C
मान लीजिए, पहले पाइप को अकेले टैंक को भरने में x घंटे लगते हैं। फिर, दूसरे और तीसरे पाइप को टैंक को भरने में क्रमशः (x-5) और (x-9) घंटे लगेंगे।
$$ ∴ {1\over x}+{1\over(x-5)}={1\over(x-9)} $$
$$⟺ \ {x-5+x\over x(x-5) }= {1\over (x-9)} $$
$$ ⟺ (2x -5)(x-9)=x(x-5)⟺ x^2-18x+45=0$$
$$ (x-15)(x-3)=0⟺ x=15. $$
Q.10. पाइप A और B एक टैंक को क्रमशः 5 और 6 घंटे में भर सकते हैं। पाइप C इसे 12 घंटे में खाली कर सकता है। यदि सभी ट्री पाइप को एक साथ खोल दिया जाए, तो टंकी कितनी भर जाएगी?
(A) ![]() hours
hours
(B) 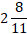 hours
hours
(C) ![]() hours
hours
(D) 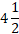 hours
hours
Ans . C
1 घंटे में भर गया शुद्ध भाग =
∴ टैंक
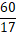 hrs में भर जाएगा यानि,
hrs में भर जाएगा यानि, 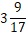 hrs.
hrs.


