बैंक पीओ के लिए समाधान के साथ सरलीकरण प्रश्न

सरलीकरण, गणित विषय का एक महत्वपूर्ण अध्याय है जिसमे अंकगणित और बीजगणित के प्रश्नों को सूत्रों या किसी नियम विशेष के आधार पर हल किया जाता है। साथ ही, वर्तमान में लगभग सभी प्रतियोगिता परीक्षा में सरलीकरण प्रश्न पूछे जाते हैं। ऐसे कई छात्र हैं जो प्रतियोगी परीक्षाओं में सरलीकरण के सवालों को हल करने में उलझन में हैं, लेकिन यदि आपके पास समाधानों के साथ सरलीकरण प्रश्नों को हल करने का एक सही तरीका है, तो परीक्षा में आपका आत्मविश्वास स्तर अपने आप बढ़ जाता है।

तो, अपने आत्मविश्वास को बढ़ाने या अपने प्रदर्शन के स्तर को बढ़ाने के लिए, एसएससी और बैंकिंग परीक्षाओं के लिए इस पोस्ट में समाधान के साथ सरलीकरण प्रश्नों को हल करना सीखें। SBI क्लर्क और अन्य बैंक परीक्षाओं से संबंधित इन सरलीकरण प्रश्नों के कारण आप अपनी परीक्षाओं के सरलीकरण प्रश्नों और उत्तरों से भी अभ्यास कर सकते हैं।

प्रतियोगी परीक्षाओं के लिए समाधान के साथ सरलीकरण प्रश्न

Q.1. 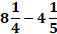 + 2.8 +   – 2.32 = 5.33

सोल्यूशन :यदि 8.25 – 4.20 +2.8 + – 2.32 = 5.33.

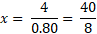तब,  = ( 5.33 + 4.20 + 2.32) – (8.25 + 2.8) = 11.85 – 11.05 = 0.80 ↔ = 5.

Q.2. 2.375 × 5.22 ÷ 0.87 – 1.425 × 0.02 = ?

सोल्यूशन:  2.375 × – 0.0285 = 2.375 × 6 – 0.0285 = 14.25 – 0.0285 = 14.2215.

Q.3. 0.2+0.2 – 0.2 ÷ 0.2 × (0.2 × 0.2), सरलीकरण पर, देता है:

सोल्यूशन:  0.2 + 0.2 – 1 × 0.04 = 0.4 – 0.04 = 0.36.

Q.4. 24-[2.4 –{.24 x 2 – (.024 - ?)}] = 22.0584

सोल्यूशन: यदि 24 – [2.4 – {.24 x 2 – (.024 – x )}] = 22.0584.

तब, 24 – {.48 - .024 + x}] = 22.0584 ↔ 24 – [2.4 – 0.456 – x ] = 22.0584

↔ 24 – 1.994 + x = 22.0584 ↔ x = 22.0584 – 22.056 = 0.0024

Q.5. 54.27 – [12.84 – {(?).87 – (3.41 × 2 – 1.85)}] = 38.33

सोल्यूशन: यदि 54.27 – [12.84 – {x – (6.82 – 1.85)}] = 38.33.

तब, 54.27 – [12.84 – {x – 4.97}] = 38.33

↔ 54.27 – [12.84 – x + 4.97] = 38.33 ↔ 54.27 – [17.81 – x ] = 38.33

↔ 54.27 – 17.81 + x = 38.33 ↔ x = 38.33 – 36.46 = 1.87.

Q.6. If 2p + 3q = 18 और 2p – q = 2, फिर 2p + q = ?

सोल्यूशन: (2p +3q) + (2p – q) = 18 +2

↔ 4p + 2q = 20 ↔ 2(2p +q) = 20

↔ 2p +q = 10.

Q.7. If 2x + y = 5 और 3x – 4y = 2, फिर 2xy का मान है: 

सोल्यूशन : 2x + y = 5………(i)       and 3x – 4y = 2

गुणा (i) 4 और जोड़कर (ii) यह, हम प्राप्त करते हैं: 11x = 22 और x = 2

Putting x = 2 in (i), हम प्राप्त करते हैं: y = 1. तो, 2xy = 2 x 2 x 1 = 4.

Q.8. If 2x + y = 17; y + 2z = 15 and x + y = 9, फिर 4x + 3y+z का मान क्या है?

सोल्यूशन : 2x + y = 17 ……….(i);  y + 2z = 15………..(ii) and x+ y = 9.

घटाव (iii) से (i), हम प्राप्त करते हैं: x = 8.

Putting x = 8 in (i); हम प्राप्त करते हैं: y = 1. Putting y = 1 in (ii), हम प्राप्त करते हैं: 2z = 14 और z = 7

  4x + 3y + z = 4 x 8 + 3 x 1 + 7 = 42.

Q.9. If 3x-4y+z = 7; 2x – z + 3y = 19; x+2y+2z = 24, फिर z का मान क्या है?

सोल्यूशन : 3x – 4y + z = 7 ……….(i); 2x + 3y – z = 19…………(ii) and x + 2y +2z = 24………….(iii)

जोड़ (i) and (ii), हम प्राप्त करते हैं: 5x – y = 26

घटाव (i) from (ii) and adding to (iii), हम प्राप्त करते हैं: 9y = 36 or y = 4

Putting y = 4 in (iv), हम प्राप्त करते हैं: 5x = 30 or x = 6.

Putting x = 6, y = 4 in (iii), हम प्राप्त करते हैं: 2z = 10 or z = 5.

Q.10. The value of 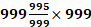 is 

सोल्यूशन: 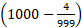 x 999 = 999000 – 4 = 998996.

यदि आपके पास कोई क्वेरी से संबंधित सरलीकरण प्रश्न हैं, तो आप मुझे बिना किसी संकोच के कमेंट बॉक्स में पूछ सकते हैं। अधिक अभ्यास के लिए अगले पेज पर जाएं।