SSC और बैंक परीक्षाओं के उदाहरणों के साथ लॉगरिदम सूत्र और समीकरण

लॉगरिदम से संबंधित प्रश्न अक्सर प्रतियोगी परीक्षाओं में क्वानटेटिव एप्टीट्यूड सेक्शन में पूछे जाते हैं, जिन्हें हल करने के लिए लॉगरिदम सूत्रों का उपयोग करना कठिन नहीं है। छात्रो को केवल फ़ार्मुलों का उपयोग करने का सही तरीका सीखने की ज़रूरत है और आपको पता होना चाहिए कि आप लॉगरिदमिक समीकरण उदाहरणों के साथ कितने प्रकार के फ़ार्मुलों का उपयोग कर सकते हैं।

इस ब्लॉग की सहायता से, आप आसानी से सीख सकते हैं कि विभिन्न लॉगरिदम समीकरणों के उदाहरणों के साथ लॉगरिदमिक सूत्रों का उपयोग कैसे करें। ये उदाहरण आपको प्रतियोगी परीक्षाओं में सूत्रों का उपयोग करने में मदद करेंगे। आप अपने बेहतर प्रदर्शन के लिए समाधान के साथ लॉगरिदमिक समस्याओं का भी अभ्यास कर सकते हैं।

प्रतियोगी परीक्षाओं के लिए लॉगरिदम सूत्र और समीकरण उदाहरण

महत्वपूर्ण तथ्य और सूत्र

1. लॉगरिदम: यदि 1 और am = x के अलावा कोई धनात्मक वास्तविक संख्या है, तो हम लिखते हैं:

m=log_ax और हम कहते हैं कि लॉग x से आधार a का मान m है।

Example :

(i) 10³=1000 → log₁₀ 1000 = 3

(ii) 3⁴=81 → log₃31 = 4

$$(iii) \ 2^{-3}={1\over8}→log_2{1\over8}=-3$$

(iv) (.1)²=.01 → log_(.1).01=2.

2. लॉगरिदम के गुण:

(i) log_a(xy)=log_ax+log_ay

(ii) log_a=log_ax-log_ay

(iii) log_xX=1

(iv) log_a1=0

(v) log_a(X^p)=p(log_aX)

$$(vi) \ log_ax={1\over log_ax}$$

$$(vii)\log_ax={log_bx\over log_ba}={logx\over loga} $$

याद रखें: जब आधार का उल्लेख नहीं किया जाता है, तो इसे 10 के रूप में लिया जाता है।

3. कॉमन लॉगरिदम: आधार 10 के लॉगरिदम को कॉमन लॉगरिदम कहा जाता है।

4. किसी संख्या के लॉगरिदम में दो भाग होते हैं, विशेषता और मंटिसा।

विशेषता: किसी संख्या के लॉगरिदम का अभिन्न अंग उसकी विशेषता कहलाता है।

केस I: जब संख्या 1 से अधिक हो।

इस मामले में, विशेषता दी गई संख्या में दशमलव बिंदु के बाईं ओर अंकों की संख्या से एक कम है।

केस II.  जब संख्या 1 से कम हो।

इस मामले में, विशेषता दशमलव बिंदु और संख्या के पहले महत्वपूर्ण अंक के बीच शून्य की संख्या से एक अधिक है और यह ऋणात्मक है।

-1 के बजाय, -2, आदि. हम लिखते है, 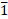(One bar) ,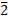(two bar), आदि.

Example:

  नंबर                   विशेषता           नंबर                 विशेषता

348.25                    2                 0.6173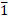                       

46.583                    1                 0.03125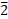                                       

9.2193                    0                 0.00125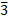                                 

मंटिसा: एक संख्या के लॉगरिदम का दशमलव भाग ज्ञात है, मंटिसा के लिए इसका मंटिसा है, हम लॉग टेबल के माध्यम से देखते हैं।

हल किए गए उदाहरण 

Ex.1. मूल्यांकन करें : (i) log₇ 1 = 0       (ii) log₃₄ 34          (iii) 36^log₆⁴

Solution 

(i) हम जानते है कि log_a 1 = 0, so log₇ 1 = 0.

(ii) हम जानते है कि log_a a = 1, so log₃₄ 34 = 0.

(iii) हम जानते है कि a^log_a^x = x

Now, 36^log₆⁴ = (6²) ^log₆⁴ = 6^2(log₆⁴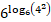⁾ = = 6^log₆¹⁶=16.

Ex.2. x का वह मान ज्ञात कीजिए जो संबंध को संतुष्ट करता है

log₁₀ 3+ log₁₀ (4x+1) = log₁₀ (x+1)+1

Solution 

log₁₀3+log₁₀(4x+1) = log₁₀(x+1)+1

⟺ log₁₀ 3 + log₁₀(4x+1)=log₁₀(x+1)+log₁₀10

⟺ log₁₀[3(4x+1)] = log₁₀[10(x+1)]

⟺ 3(4x+1) = 10(x+1) ⟺ 12x + 3 = 10x +10 ⟺ 2x = 7 ⟺ 

Ex.3. $$Simplifv =   \left({1\over log_{xy}(xyz)}+{1\over log_{yz}(xyz)}+{1\over log_{zx}(xyz)}\right)$$

Solution

दी गई अभिव्यक्ति = log_xyz(xy) + log_xyz(yz) +log_xyz(zx)

= log_xyz(xy × yz × zx) = log_xyz(xyz)²

  $$∴ \left(log_ax={1\over log_xa}\right)$$ = 2 log_xyz(xyz) = 2 × 1 = 2.

Ex.4. यदि log₁₀ 2 = 0.30103, log₁₀50 का मान ज्ञात कीजिए।

Solution

$$log_{10}50=log_{10}\left({100\over2}\right)=log_{10}100-log_{10}2 = 0.30103 = 1.69897$$

Ex.5. यदि log 2 = 0.30103, 2⁵⁶ में अंकों की संख्या ज्ञात कीजिए।

Solution 

Log(2⁵⁶)=56 log 2 = (56 × 0.30103) = 16.85768.

इसकी विशेषता 16 है। अत:  2⁵⁶  में अंकों की संख्या 17 है।

अगर आपको इन लॉगरिदमिक फ़ार्मुलों में कोई समस्या आती है या लॉगरिदमिक समीकरणों के उदाहरणों और सूत्रों के बारे में कुछ भी पूछना चाहते हैं, तो आप मुझसे कमेंट बॉक्स में पूछें। यदि आप उत्तर के साथ लॉगरिदम प्रश्नों का अधिक अभ्यास करना चाहते हैं तो यहाँ जाएँ।