SSC और बैंक परीक्षाओं के लिए समाधान के साथ लघुगणक समीकरण उदाहरण

लघुगणक क्वानटेटिव एप्टीट्यूड प्रश्न अक्सर प्रतियोगी परीक्षाओं में पूछे जाते हैं। लघुगणक समस्याओं को हल करने में अधिकांश छात्रों को कठिनाइयों का सामना करना पड़ता है क्योंकि वे समाधान के साथ लघुगणक समस्याओं का अभ्यास नहीं करते हैं।

यहां इस ब्लॉग में, आप समाधान के साथ लघुगणक समस्याओं की अपनी कठिनाइयों को आसानी से हल कर सकते हैं। इसलिए लघुगणक समस्याओं को स्वयं आसानी से हल करने का प्रयास करें और समाधान के साथ लघुगणक समस्याओं को हल करना सीखें।

सीखने के बाद आप ssc और बैंक परीक्षाओं के उत्तरों के साथ लघुगणक प्रश्नों के साथ अधिक अभ्यास कर सकते हैं और अपने प्रदर्शन स्तर को भी सुधार सकते हैं।

प्रतियोगी परीक्षाओं के समाधान के साथ लघुगणकीय समस्याएं:

लघुगणक समीकरण उदाहरण और समाधान के साथ समस्याएं

Q.1. log₃₄₃ 7 का मान है :

$$(a) \ {1\over3} \ (b) \ -3\ (c) \  -{1\over3}\ (d) \ 3 $$

समाधान:

Let log₃₄₃ 7 = n. Then, (343)ⁿ = 7 ↔ (7³)ⁿ = 7 ↔ 3n= 1

$$  ↔n={1\over3}.$$ $$∴ log_{343}7={1\over3}$$

Q.2. log_√232 का मान है : 

$$(a) \ {5\over2} \ (b) \ 5\ (c) \  10\ (d) \ {1\over10} $$

समाधान:

Let log√₂32=n. Then, (√2)ⁿ=32↔(2)^n/2=2⁵

$$  ↔{n\over2}=5↔n=10.$$ $$∴ log_\sqrt{2}32=10.$$

Q.3. log_(.01)(1000) का मान है :

$$(a) \ {1\over3} \ (b) \ -{1\over3}\ (c) \  {3\over2}\ (d) \ -{3\over2}\  $$

समाधान:

Let log_(.01) (1000) = n.

Then, (.01)ⁿ = 1000

$$↔ \left({1\over100}\right)^n=10^3$$

↔ (10^-2n) = 10³↔ - 2n=3 $$↔ n=-{3\over2}$$

Q.4. यदि log₃x = - 2, तो x बराबर है :

$$(a) \ -9 \ (b)-6 \   (c) \ -8 \ (d) \ {1\over9}\  $$

समाधान:

Log₃x = -2 ↔ x = 3^-2$$={1\over3^2}={1\over9}$$

Q.5. यदि log_x =  , तो x बराबर है : 

$$(a) \ -{3\over4} \ (b)\ {3\over4} \  (c) \ {81\over256} \ (d) \ {256\over81}\  $$

समाधान:

   $$log_x=\left({9\over16}\right)=-{1\over2}⟺x^{-1/2}={9\over16}$$

  $${1\over \ \sqrt x\ }={9\over16}⟺ \sqrt x\ = {16\over9}$$

$$x=\left({16\over9}\right)^2={256\over81}$$

Q.6. log₂ 16 का मान है :

$$(a) \ {1\over8} \ (b) \ 4\ (c) \ 8\ (d) \ 16 $$

समाधान:

Let log₂ 16 = n. Then, 2ⁿ = 16 = 2⁴→n=4.

∴ log₂ 16 = n.

Q.7. log₅  का मान है :

$$(a) \ 3 \ (b) \ -3\ (c) \  {1\over3}\ (d) \ -{1\over3} $$

समाधान:

$$ Let \ log_5\left({1\over125}\right)=n.$$

   $$Then, 5^n={1\over125}↔ 5^n= 5^{-3}↔n=-3$$

   $$∴ log_5\left({1\over125}\right)=-3.$$

Q.8. log₁₀(.0001) का मान है :

$$(a) \ {1\over4} \ (b) \ -{1\over4}\ (c) \  -4\ (d) \ 4 $$

समाधान:

Let log₁₀(.0001)=n.

Then, 10ⁿ = 0.001

$$ ↔10^n={1\over1000}={1\over10^4}$$

↔ 10n=10^–4 ↔ n = -4.

∴ log₁₀ (.0001) =-4

Q.9. आधार 2 का 0.0625 का लघुगणक है :

$$(a) \ -4 \ (b)-2 \  (c) \ 0.25   \ (d) \ .5\  $$

समाधान:

Let log₂0.0625 = n. Then 2n = 0.0625

$$={625\over10000}↔2^n={1\over16}↔2^n=2^{-4}↔n=-4.$$

∴ log₂ 0.0625= - 4 

Q10. यदि log₈ x= , फिर x का मान है:

$$(a) \ {3\over4} \ (b)\ {4\over3} \  (c) \ 3 \ (d) \ 4\  $$

समाधान:

$$log_8x={2\over3}↔x=8^{2/3}=(2^3)^{2/3}$$

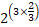==2²=4

मुझे आशा है कि ये समाधान आपकी तैयारी के लिए सहायक होंगे। यदि आपको लघुगणक समीकरणों के उदाहरणों और समाधानों के साथ समस्याओं के बारे में कोई समस्या या संदेह है या आप कोई प्रश्न पूछना चाहते हैं, तो आप मुझसे कमेंट बॉक्स में पूछ सकते हैं।

आपकी परीक्षा के लिए शुभकामनाएं