बैंक परीक्षाओं के लिए सामान्य गणित के प्रश्न
यदि (A+B) का 40% = (A-B) का 60% तो $${2A-3B}\over {A+B}$$ किसके बराबर होगा?
(A) $${7\over 6}$$
(B) $${6\over 7}$$
(C) $${5\over 6}$$
(D) $${6\over 5}$$
Correct Answer : A
Explanation :
₹10000 के $$33{1\over 3}\%$$ का 0.15% कितना होगा :
(A) ₹ 5
(B) ₹ 150
(C) ₹ 0.05
(D) ₹ 105
Correct Answer : A
Explanation :
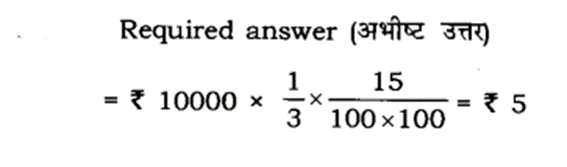
यदि $${25\over 2}\%$$ का x% ,150 है, तो x का मान है:
(A) 1000
(B) 1200
(C) 1400
(D) 1500
Correct Answer : B
Explanation :
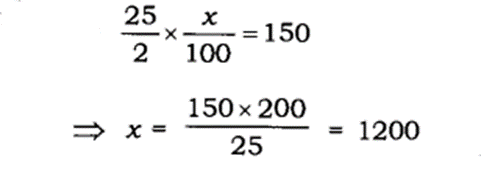
यदि (x-y) का 50% = (x+y) का 30%, तो x का कितना प्रतिशत y है?
(A) 25%
(B) $$33{1\over 3}\%$$
(C) 40%
(D) 400%
Correct Answer : A
Explanation :
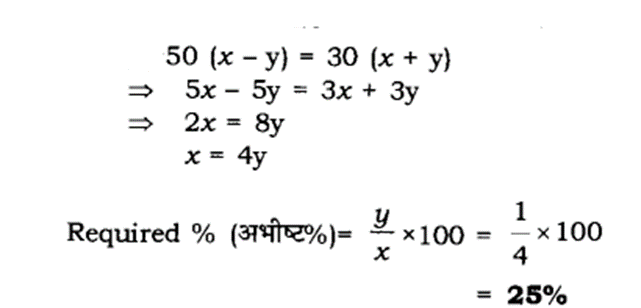
What percent of 3.6kg is 72 gms ?
(A) 32%
(B) 22%
(C) 12%
(D) 2%
Correct Answer : D
Explanation :
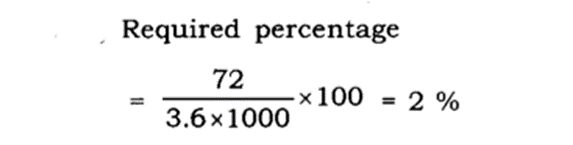
A, B से 25% अधिक तेजी से यात्रा करता है। उन्होंने एक बिंदु P से दूसरे बिंदु Q तक अपनी यात्रा शुरू की और बिंदु Q पर एक ही समय पर पहुंचे। P और Q के बीच की दूरी 85 किमी है। तथापि, मार्ग में, A को पेट्रोल के लिए रुकते समय लगभग 20 मिनट का समय गंवाना पड़ा। B की गति क्या थी?
(A) 51 किमी/घंटा
(B) 50 किमी/घंटा
(C) 45 किमी/घंटा
(D) 75 किमी/घंटा
(E) इनमें से कोई नहीं
Correct Answer : A
स्थिर जल में नाव की गति 9 किमी/घंटा है। धारा की गति प्रारंभ में 2 किमी/घंटा है लेकिन यह प्रत्येक घंटे के बाद 3 किमी/घंटा बढ़ जाती है। कितने समय के बाद नाव वापस उसी स्थान पर आ जाएगी जहां से वह चलना शुरू हुई थी। (घंटे में)
(A) 5(5/8)
(B) 4(7/8)
(C) 5(3/8)
(D) 4(3/4)
(E) इनमें से कोई नहीं
Correct Answer : A
अखिल को 150 किमी की दूरी तय करने में 30 मिनट अतिरिक्त लगते हैं यदि वह अपनी सामान्य गति से 10 किमी/घंटा धीमी गति से ड्राइव करता है। यदि वह अपनी सामान्य गति से 15 किमी प्रति घंटा धीमी गति से गाड़ी चलाता है तो उसे 90 किमी की दूरी तय करने में कितना समय लगेगा?
(A) 2 घंटे 45 मी
(B) 2 घंटे 30 मी
(C) 2 घंटे
(D) 2 घंटे 15 मी
Correct Answer : C
Explanation :
पहले हमें अखिल की सामान्य गति को पता करने की आवश्यकता है:
हम जानते हैं कि अखिल को अपनी सामान्य गति से 150 किमी की दूरी को तय करने में 30 मिनट (0.5 घंटे) अधिक लगते हैं, जब वह अपनी सामान्य गति से 10 किमी/घंटा से धीमी गति से चलाता है।
"S" को अखिल की सामान्य गति के रूप में दर्शाते हैं। इसलिए, उसकी धीमी गति (S - 10) किमी/घंटा होगी।
दूरी को तय करने के लिए समय, दुरी को गति से विभाजित करने से प्राप्त होता है: समय = दूरी / गति
उसकी सामान्य गति पर, उसको लगता है: समय सामान्य गति पर = 150 किमी / S घंटे
उसकी धीमी गति पर, उसको लगता है: समय धीमी गति पर = 150 किमी / (S - 10) घंटे
इन दो परिस्थितियों के बीच समय का अंतर 0.5 घंटे (30 मिनट) होता है: समय धीमी गति पर - समय सामान्य गति पर = 0.5 घंटे
अब, हम इस मसले को हल करने के लिए समीकरण बना सकते हैं और S के लिए हल कर सकते हैं:
(150 किमी / (S - 10)) - (150 किमी / S) = 0.5
इस समीकरण को हल करने के लिए, हम पहले एक सामान्य मामाये को प्राप्त करते हैं: (150S - 150(S - 10)) / (S(S - 10)) = 0.5
अब, सरलीकरण करें और S के लिए हल करें: (150S - 150S + 1500) / (S(S - 10)) = 0.5
(1500) / (S(S - 10)) = 0.5
अब, पार करने के लिए दोनों पक्षों को 4 से विभाजित करें: 4(S(S - 10)) = 1500
S(S - 10) = 1500 / 4 S(S - 10) = 375
अब, हम S के लिए इस समीकरण को हल कर सकते हैं:
S^2 - 10S - 375 = 0
अब, हम S के लिए इस द्विघातक समीकरण को हल कर सकते हैं:
S = [-(-10) ± √((-10)^2 - 4(1)(-375))] / (2(1))
S = [10 ± √(100 + 1500)] / 2
S = [10 ± √1600] / 2
S = [10 ± 40] / 2
अब, हमारे पास S के लिए दो संभावित मूल हैं, लेकिन हम गति को नकारात्मक नहीं ले सकते हैं क्योंकि गति नकारात्मक नहीं हो सकती है:
S = (10 + 40) / 2 = 50 / 2 = 25 किमी/घंटा
इसलिए, अखिल की सामान्य गति 25 किमी/घंटा है।
अब, हम जानना चाहते हैं कि वह 15 किमी/घंटा की गति से चलाने पर 90 किमी को तय करने में कितना समय लगेगा, जो कि उसकी सामान्य गति से 15 किमी/घंटा कम होगी, जो कि (25 - 15) = 10 किमी/घंटा होगी।
समय = दूरी / गति समय = 90 किमी / 10 किमी/घंटा = 9 घंटे
अखिल को 15 किमी/घंटा की गति से चलाते हुए 90 किमी को तय करने में 9 घंटे लगेंगे।
3 किमी / घण्टा की गति से दौड़ते हुए, एक व्यक्ति अपने गन्तव्य पर सामान्य समय से 10 मिनट देर से पहुँचता है। यदि वह अपनी गति 1 किमी/घण्टा बढ़ाता है, तो वह अपने गन्तव्य पर 15 मिनट पहले पहुँचता है। उसके गन्तव्य तक की दूरी ज्ञात कीजिए।
(A) 10 km
(B) 12 km
(C) 5 km
(D) 4 km
(E) इनमें से कोई नहीं
Correct Answer : C
एक आदमी 10 घण्टे में धारा के प्रतिकूल 52 किमी और धारा के अनुकूल 42 किमी की दूरी तय कर सकता है। यह भी ज्ञात है कि वह धारा के अनुकूल 66 किमी और धारा के प्रतिकूल 60 किमी 13 घण्टे में तैर सकता है। शान्त जल में व्यक्ति की गति ज्ञात कीजिए।
(A) 8 किमी/घंटा
(B) 12 किमी/घंटा
(C) 6 किमी/घंटा
(D) 10 किमी/घंटा
(E) इनमें से कोई नहीं
Correct Answer : D
Showing page 2 of 4
hnhttps://www.hindi.examsbook.com/general-math-questions-for-bank-exams/242general-math-questions-for-bank-examsलेखक के बारे में
Rajesh Bhatia
A Writer, Teacher and GK Expert. I am an M.A. & M.Ed. in English Literature and Political Science. I am highly keen and passionate about reading Indian History. Also, I like to mentor students about how to prepare for a competitive examination. Share your concerns with me by comment box. Also, you can ask anything at linkedin.com/in/rajesh-bhatia-7395a015b/.
और अधिक पोस्ट पढ़ें