प्रतियोगी परीक्षाओं के समाधान के साथ एनालिटिकल रीजनिंग प्रश्न
एनालिटिकल प्रश्नों में कॉम्प्लेक्स फिगर से ज्योमैट्रिकल फिगर्स को गिनते समय छात्रों को अक्सर समस्या का सामना करना पड़ता है क्योंकि वे भ्रमित हो जाते हैं। चिंता न करें, यह इतने कठिन सवाल नहीं है। शुरुआत में, आपको एनालिटिकल रीजनिंग वाले प्रश्नों को हल करना मुश्किल होगा, लेकिन यदि आप इस टॉपिक को ठीक से तैयार कर रहे हैं, तो कुछ समय बाद आप इस प्रकार के प्रश्नों को आसानी से हल कर सकेंगे।
तो, यहाँ इस ब्लॉग में समाधान के साथ ऐसे ही एनालिटिकल रीजनिंग प्रश्न दिए जा रहे हैं जो आपके प्रदर्शन के साथ-साथ आपके आत्मविश्वास को बेहतर बनाने में मदद करेंगे।
हिंदी प्रश्नों में एनालिटिकलरीजनिंग की जाँच करें।
समाधान के साथ एनालिटिकल समस्याएं:
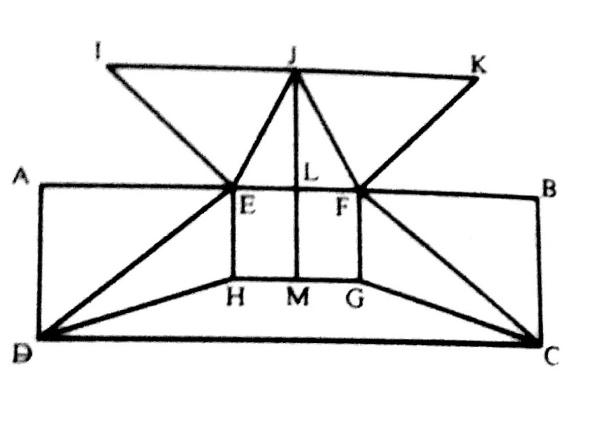
Q.1.
(A) 16
(B) 17
(C) 18
(D) 19
Ans . B
1. चित्र को दिखाए अनुसार लेबल किया जा सकता है। क्षैतिज रेखाएँ IK, AB, HG और DC अर्थात् संख्या में 4 हैं। ऊर्ध्वाधर रेखाएँ AD, EH, JM, FG और BC हैं अर्थात् संख्या में 5। तिरछी रेखाएँ IE, JE, JF, KE, DE, DH, FC और GC अर्थात् 8 की संख्या में हैं। इस प्रकार, आकृति में 4 + 5 + 8 17 सीधी रेखाएं हैं।
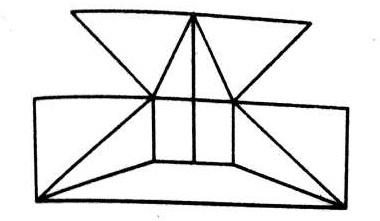
Q.2.
(A) 11
(B) 14
(C) 16
(D) 17
Ans . B
2. चित्र को दिखाए अनुसार लेबल किया जा सकता है। क्षैतिज रेखाएँ AK, BJ, CI, DH और EG हैं जो संख्या में 5 हैं। खड़ी रेखाएँ AE, LF और KG हैं अर्थात् संख्या 3 में। तिरछी रेखाएँ LC, CF, FI, LI, EK और AG हैं अर्थात् संख्या में 6, इस प्रकार चित्रा में 5 + 3 +6 14 सीधी रेखाएँ हैं।
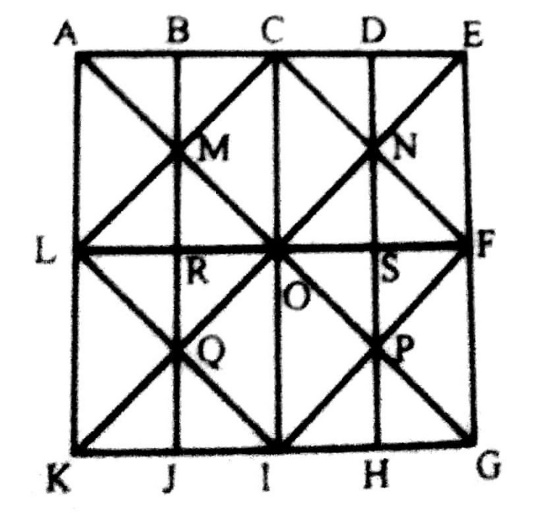
Q.3.
(A) 9
(B) 11
(C) 15
(D) 16
Ans . B
3. हम चित्र को दिखाए गए अनुसार लेबल करेंगे। क्षैतिज रेखाएँ DE, FH, IL और BC हैं अर्थात् संख्या में 4। तिरछी रेखाएँ हैं AC, DO, PN, IM, AB, EM और HN यानि संख्या 7। इस प्रकार, आकृति में 4 + 7 = 11 सीधी रेखाएं हैं।
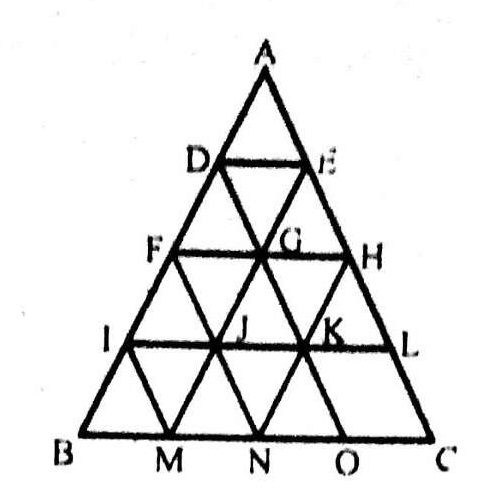
Q.4.
(A) 13
(B) 15
(C) 17
(D) 19
Ans . A
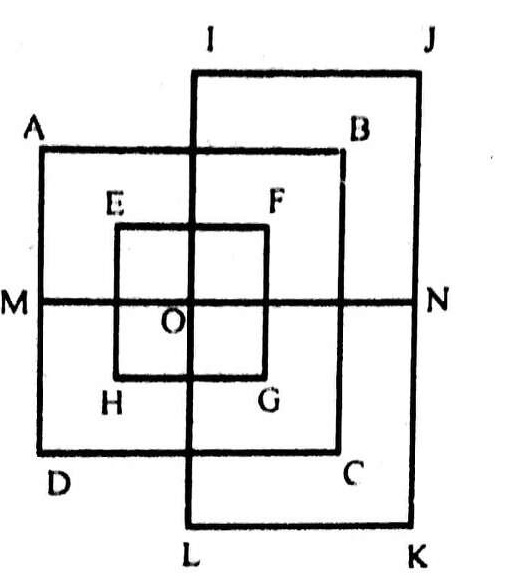
4. चित्र को दिखाए अनुसार लेबल किया जा सकता है। क्षैतिज रेखाएँ IJ, AB, EF, MN, HG, DC और LK हैं अर्थात् संख्या में 7। ऊर्ध्वाधर रेखाएँ AD, EH, IL, FG, BC और JK हैं अर्थात् संख्या में 6। इस प्रकार, आकृति में 7 + 6 = 13 सीधी रेखाएं हैं।
Q.5.
(A) 4
(B) 5
(C) 6
(D) 7
Ans . B
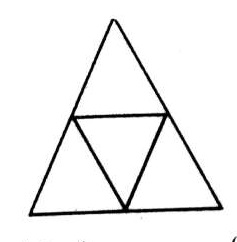
5. हम चित्र को दिखाए गए अनुसार लेबल कर सकते हैं। सबसे सरल त्रिकोण हैं ADE, BDF, DEF और EFC यानी संख्या में 4। चार घटकों से बना केवल एक त्रिभुज ABC है, इस प्रकार, दिए गए चित्र में 4 + 1 = 5 त्रिकोण हैं।
Q.6.
(A) 5
(B) 6
(C) 8
(D) 10
Ans . A
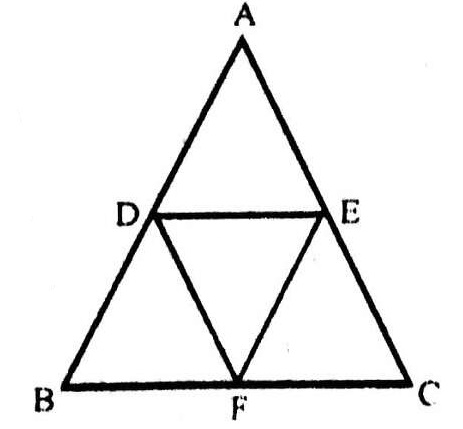
6. चित्र को दिखाए अनुसार लेबल किया जा सकता है। सबसे सरल त्रिकोण AJF, FBG, GCH, HDI और IEJ यानी संख्या में 5 हैं। त्रिभुज तीन घटकों से बने होते हैं जिनमें प्रत्येक EBH, AIC, EFC, ADG और BJD यानी संख्या में 5। इस प्रकार, आकृति में 5 + 5 = 10 त्रिकोण हैं।
Q.7.
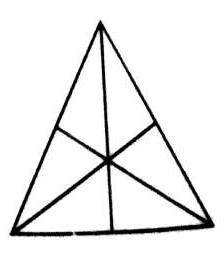
(A) 16
(B) 13
(C) 9
(D) 7
Ans . A
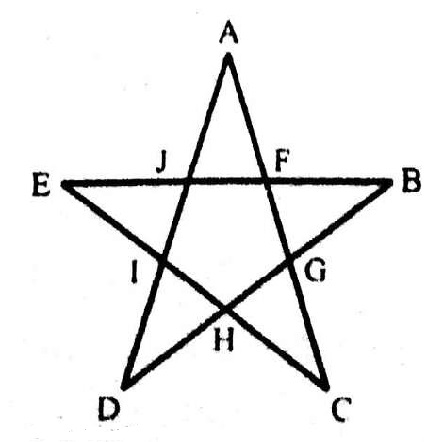
7. चित्र को दिखाए अनुसार लेबल किया जा सकता है। सबसे सरल त्रिकोण हैं AGE, EGC, GFC, BGF, DGB और ADG यानी संख्या में 6। प्रत्येक दो घटकों से बने त्रिकोण एजीसी, बीजीसी और एबीजी हैं अर्थात् संख्या में 3। प्रत्येक तीन घटकों से बने त्रिकोण AFC, BEC, BDC, ABF, ABE और DAC यानी संख्या में 6 हैं। केवल एक त्रिभुज है यानी ABC छह घटकों से बना है। इस प्रकार, दिए गए आंकड़े में 6 + 3 + 6 + 1 = 16 त्रिकोण हैं।
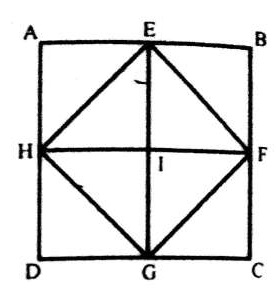
Q.8
(A) 15
(B) 16
(C) 17
(D) 18
Ans . C
8. चित्र को दिखाए अनुसार लेबल किया जा सकता है। सबसे सरल त्रिकोण ABF, BFG, BCG, CGH GHD, GED, EFG और AFE यानि 8 की संख्या में हैं। प्रत्येक दो घटकों से बना त्रिकोण ABG, BGE, AGE, ABE और GCD यानी 5 की संख्या में हैं। प्रत्येक तीन घटकों से बना त्रिकोण BCD, CDE, BED और BCE यानी संख्या में 4 हैं। इस प्रकार, आकृति में 8 + 5 + 4 = 17 त्रिकोण हैं।
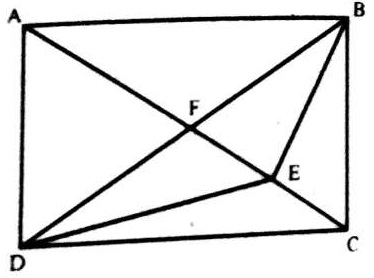
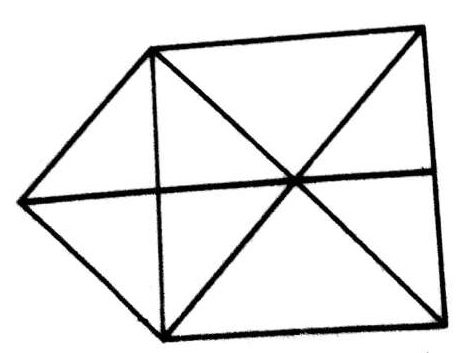
Q.9.
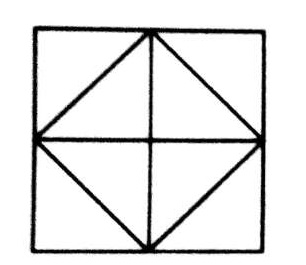
(A) 8
(B) 10
(C) 12
(D) 14
Ans . C
9. चित्र को दिखाए अनुसार लेबल किया जा सकता है। सबसे सरल त्रिभुज AEH, EHI, EBF, EFI, FGC, IFG, DGH और HIG हैं, अर्थात् संख्या में 8। त्रिकोण दो घटकों से बना है HEF, EFG, HFG और EFG अर्थात् संख्या में 4 हैं। इस प्रकार आकृति में 8 + 4 = 12 त्रिकोण हैं।
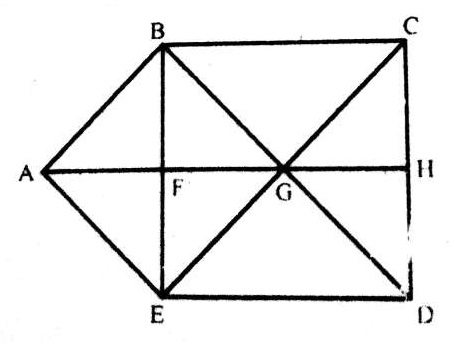
Q.10.
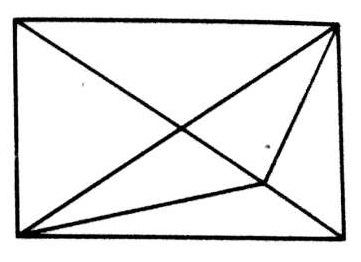
(A) 11
(B) 13
(C) 15
(D) 17
Ans . C
10. हम चित्र को दिखाए गए अनुसार लेबल कर सकते हैं। सबसे सरल त्रिभुज हैं AFG, FEB, EBC, DEC, DFE और AFD यानी संख्या में 6। तीन घटकों से बना त्रिकोण प्रत्येक ADC और ABC है अर्थात् संख्या में 2। केवल एक त्रिभुज है यानी DBC जो चार घटकों से बना है। इस प्रकार, तीन 6 + 6 + 2 + 1 = 15 त्रिकोण हैं।
About author
Vikram Singh
Providing knowledgable questions of Reasoning and Aptitude for the competitive exams.
Read more articles