SSC और बैंक परीक्षा के लिए समाधान के साथ क्यूब समस्याएं

प्रतियोगी परीक्षा में क्यूब एक महत्वपूर्ण टॉपिक है क्योंकि हर साल इस टॉपिक से प्रश्न पूछे जाते हैं। यहां पर विभिन्न क्यूब समस्याओं के समाधानों के बारे में बताया गया है, जिसमें से आप प्रतियोगी परीक्षाओं में इस प्रकार के प्रश्नों को आसानी से हल कर सकते हैं।
तो, समाधान के साथ इन कुछ क्यूबसमस्याओं को देखते हुए अपना अभ्यास जारी रखें, जो आपको प्रतियोगी परीक्षा में अपने स्कोर को बेहतर बनाने में मदद करेगा। समाधान के साथ स्क्वायर रूट और क्यूब रूट समस्याओं को हल करने के लिए यहां क्लिक करें।
प्रतियोगी परीक्षाओं के लिए क्यूब समस्याएं और समाधान
क्यूब क्या है?
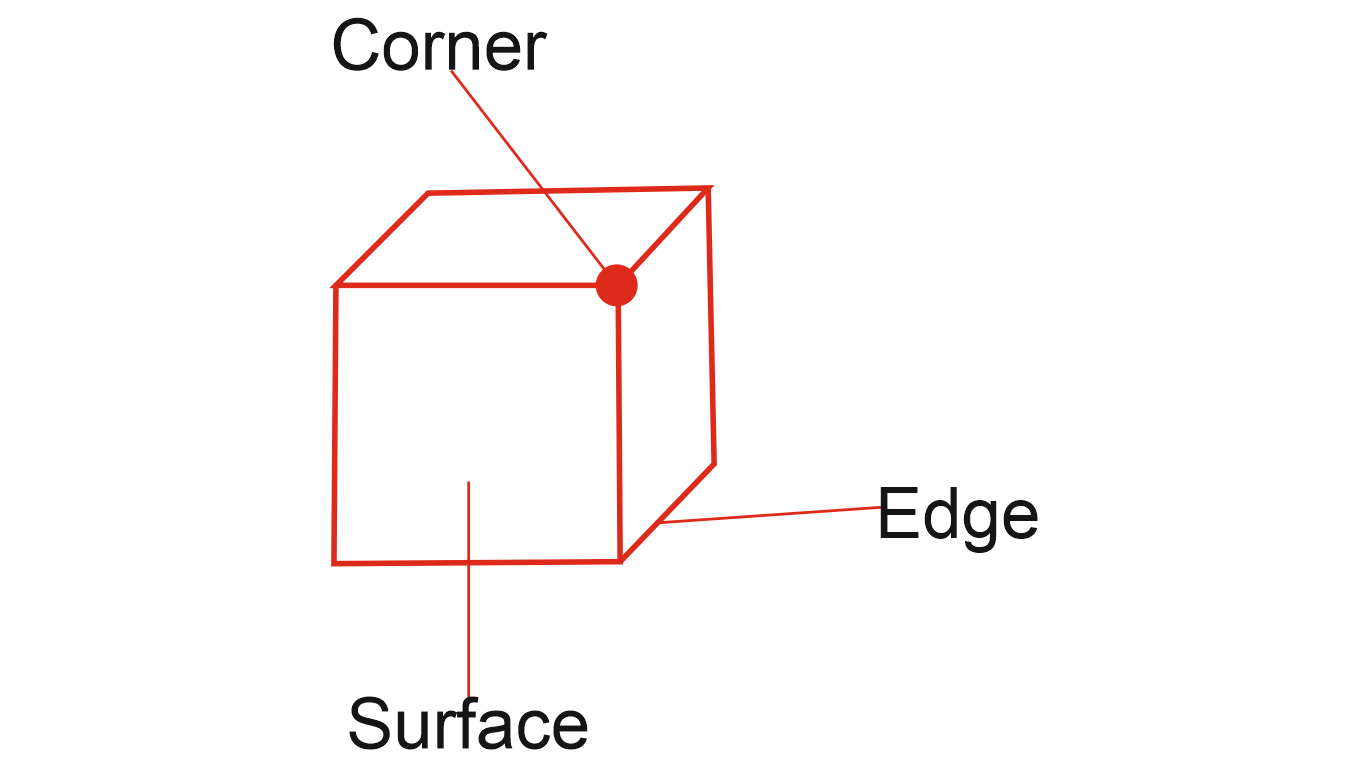
एक क्यूब एक तीन आयामी ठोस होता है जिसमें 6 चेहरे, 12 किनारे और 8 कोने होते हैं। एक क्यूब्स के सभी किनारे समान हैं और इसलिए सभी चेहरे आकार में चौकोर हैं।
क्यूब्स पर प्रश्न निम्नलिखित श्रेणियों में से किसी से संबंधित हो सकते हैं:
1. निश्चित संख्या में कटौती करके एक क्यूब काट दिया जाता है। जिन दिशाओं में कटौती की गई है, वे दिए जा सकते हैं या नहीं। हमें दिए गए कट से निकलने वाले समान टुकड़ों की संख्या का पता लगाना है।
2. समान टुकड़ों की संख्या, जिसमें एक क्यूब काट दिया जाता है, दिया जाता है और हमें कटौती की संख्या खोजने की आवश्यकता है।
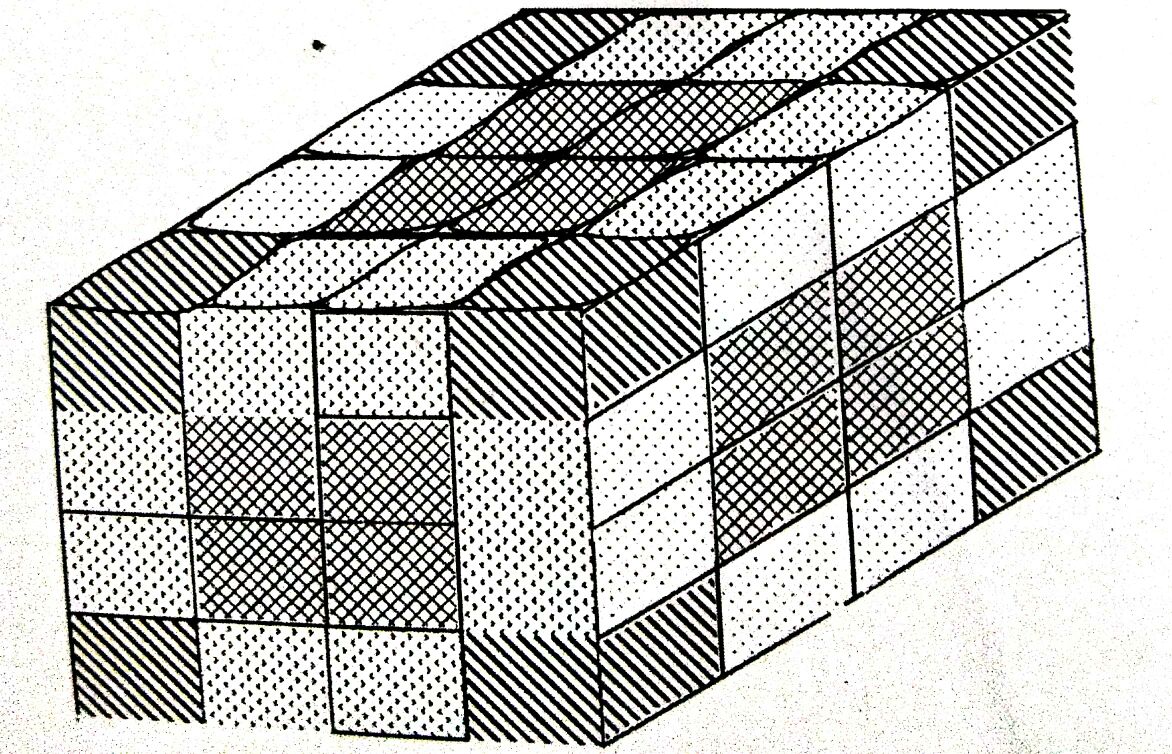
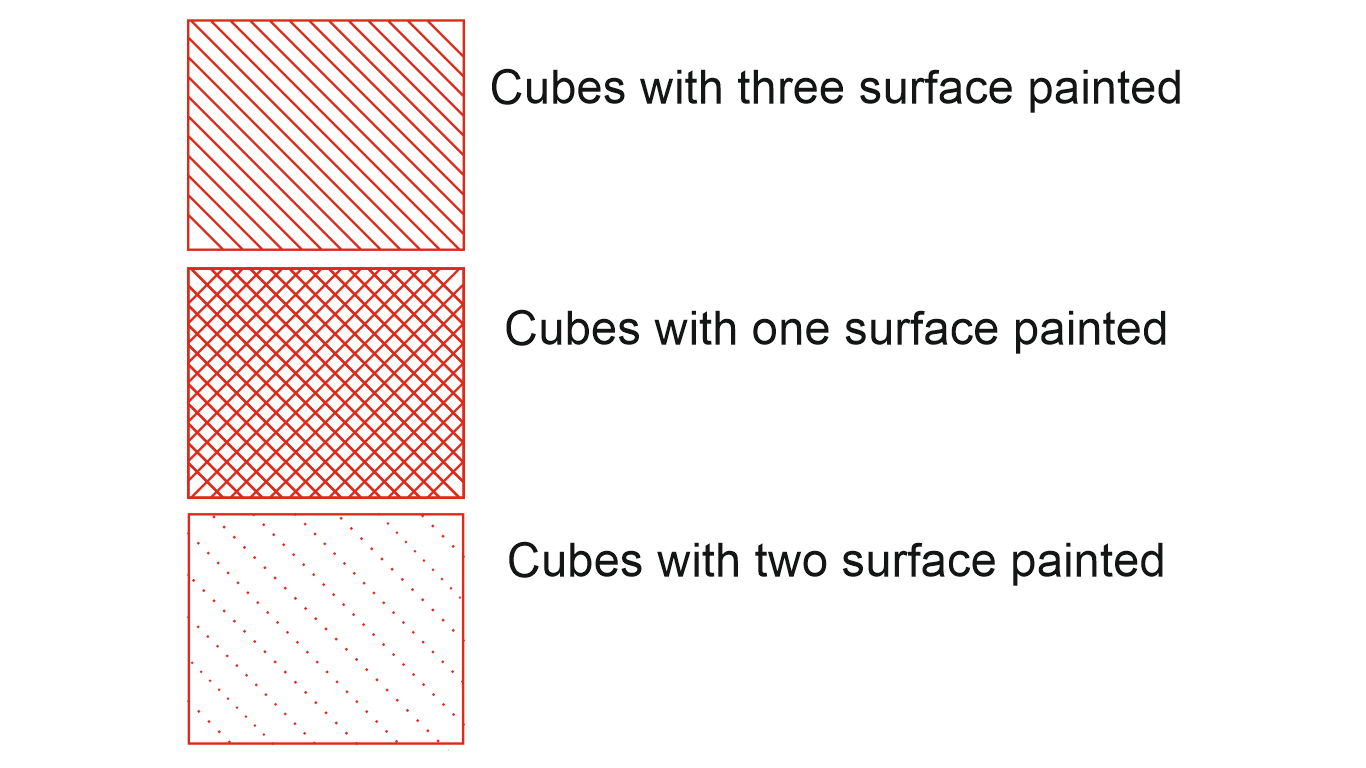
3. एक घन सभी या उसके चेहरे पर एक ही रंग या अलग-अलग रंगों के साथ चित्रित किया जा सकता है और फिर एक निश्चित निर्दिष्ट संख्या में समान टुकड़ों में काटा जा सकता है। फॉर्म के प्रश्न- "कितने छोटे क्यूब्स में 2 चेहरे चित्रित हैं?" "कितने छोटे क्यूब्स में केवल एक ही चेहरा चित्रित किया गया है?" आदि के बाद फंसाया जा सकता था।
क्यूब्स से संबंधित प्रश्नों को हल करने के लिए आपको दिए गए नियमों का पालन करना चाहिए। दिए गए नियम प्रश्नों को हल करने में उपयोगी शॉर्टकट्स को याद करने में आपकी मदद करते हैं।
यदि एक घन को सभी छह सतहों पर चित्रित किया जाता है और समान संख्या में x को काट दिया जाता है, तो
1. कोई सतह की ओर इशारा करते हुए क्यूब्स की संख्या = (n - 2)3
2. एक सतह को चित्रित करने वाले क्यूब्स की संख्या (n - 2)2 x 6
3. दो सतहों को चित्रित करने वाले क्यूब्स की संख्या (n- 2) x 12.
4. तीन सतहों को चित्रित करने वाले क्यूब्स की संख्या = 8
5. एक घन नहीं हो सकता है जिसमें तीन से अधिक सतहें चित्रित हैं।
Note : - यदि किसी पक्ष के 'a' सेमी को टुकड़ों में काटा जाता है जैसे कि छोटे घन का प्रत्येक भाग "b" सेमी का तो $ $ n= \left({a\over b}\right)^3$$
Q.1. एक घन को उसके चेहरे के समानांतर एक समतल के साथ दो बराबर भागों में काटा जाता है। एक टुकड़ा फिर दो बड़े चेहरों पर लाल और शेष पर हरे रंग का होता है जबकि दूसरा दो छोटे आसन्न चेहरों पर हरा और शेष पर लाल रंग का होता है। प्रत्येक को फिर एक ही आकार के 32 क्यूब्स में काट दिया जाता है। 64 क्यूब्स को फिर मिश्रित किया जाता है।
Q.1. कितने क्यूब्स में कोई रंगीन चेहरा नहीं है?
(A) 16
(B) 8
(C) 4
(D) 0
Ans . D
दोनों ढेर में, कोई घन नहीं है जिसका कोई रंगीन चेहरा नहीं है।
Q.2. कितने घन में केवल एक रंगीन चेहरा होता है?
(A) 8
(B) 16
(C) 20
(D) 24
Ans . D
स्टैक A में दो परतों A2 और A3 में से प्रत्येक में चार क्यूब्स (कॉलम a3, a4, a5 और a6) और इसी तरह चार क्यूब्स (कॉलम b3, b4, b5 और b6 में) प्रत्येक दो B2 और B3 में समान हैं। स्टैक B में केवल एक रंगीन चेहरा है।
इस प्रकार, (4 x 2) + (4 x 2) = 8 + 8 16 ऐसे घन हैं।
Q.3. कितने क्यूब्स में दो लाल और एक हरा चेहरा होता है?
(A) 4
(B) 8
(C) 12
(D) 16
Ans . A
स्टैक A में कोई क्यूब नहीं है जिसमें दो लाल चेहरे हैं। स्टैक B में लेयर B4 में दो क्यूब्स (कॉलम b7 और b8 में) और स्टैक B में लेयर B4 में दो क्यूब्स (कॉलम b1 और b2 में) के दो लाल और एक हरे रंग का चेहरा होता है।
इस प्रकार, (2 + 2)= 4 ऐसे घन हैं।
Q.4. कितने क्यूब्स में एक चेहरा लाल दूसरा हरा है?
(A) 32
(B) 24
(C) 16
(D) 8
Ans . B
दो परतों A1 और A4 में से प्रत्येक में चार क्यूब्स (कॉलम a3, a4, a5 और a6) और चार क्यूब्स में (कॉलम a1, a2, a7 और a8) प्रत्येक दो परतों में A3 और A4 में से प्रत्येक में एक है। चेहरा लाल और दूसरा चेहरा हरा।
परत बी 1 में चार क्यूब्स (कॉलम b3, b4, b5 और b6) और स्टैक बी में बी 2 और बी 3 में से प्रत्येक में दो क्यूब्स (कॉलम b1 और b2 में) एक चेहरा लाल और दूसरा हरा होता है। इस प्रकार, (4 x 2) + (4 x 2)+ 4+ (2 x 2) = 8+ 8+4+4 24 ऐसे घन हैं।
Q.5. कम से कम एक हरे रंग के चेहरे के साथ क्यूब्स की संख्या क्या है?
(A) 46
(B) 38
(C) 36
(D) 28
Ans . B
आठ क्यूब्स (कॉलम a1, a2, a4, a5, a6, a7 और a8) में से प्रत्येक में दो लेयर A1 और A4 और चार क्यूब्स (कॉलम a1, a2, a7 और a8) दोनों में से प्रत्येक में। स्टैक ए में लेयर ए 2 और ए 3 में कम से कम एक हरा चेहरा होता है।
लेयर B1 और दो क्यूब्स (कॉलम b1 और b2 में) तीन परतों B2, B3 और B4 में से प्रत्येक में आठ क्यूब्स (कॉलम b1, b2, b3, b4, b5, b6, b7, b8) स्टैक B में B3 और B4 में से प्रत्येक में हैं। कम से कम एक हरा चेहरा।
इस प्रकार, (8 x 2)+(4 x 2)+8 (23) = 16+8+8+6 = 38 ऐसे घन हैं।
यदि आप किसी भी संबंधित घन समस्या और उसके समाधान पूछना चाहते हैं, तो आप मुझसे कमेंट बॉक्स में पूछ सकते हैं। अधिक अभ्यास के लिए अगले पेज पर जाएँ।



