एसएससी और बैंक परीक्षा के लिए समाधान के साथ चक्रवृद्धि ब्याज की समस्याएं

आमतौर पर प्रतियोगी परीक्षाओं में पूछे जाने वाले चक्रवृद्धि ब्याज की समस्याएं। एसएससी और बैंक परीक्षा के लिए ये चक्रवृद्धि ब्याज की समस्याएं बहुत महत्वपूर्ण हैं। तो आपको सीखना चाहिए कि ssc और बैंक परीक्षाओं के समाधान के साथ चक्रवृद्धि ब्याज की समस्याओं को कैसे हल किया जाए।

यहां इस ब्लॉग में, आप आसानी से सीख सकते हैं कि उदाहरणों और विभिन्न -2 समीकरणों के साथ चक्रवृद्धि ब्याज की समस्याओं को कैसे हल किया जाए। आप उदाहरणों के साथ चक्रवृद्धि ब्याज सूत्रों का उपयोग करके सीख सकते हैं और अपने प्रदर्शन स्तर को उज्ज्वल कर सकते हैं।

आपको हल किए गए उदाहरणों की जांच करनी चाहिए ताकि आप आसानी से समझ सकें कि सरल और चक्रवृद्धि ब्याज प्रश्नों को हल करते समय फॉर्मूलों का उपयोग कैसे करें।

प्रतियोगी परीक्षाओं के लिए समाधान के साथ चक्रवृद्धि ब्याज की समस्याएं

Q.1 अल्बर्ट ने 5 p.c.p.a. चक्रवृद्धि ब्याज दर पर 5 वर्षों के लिए फिक्स्ड डिपॉजिट स्कीम में 8000रु की राशि का निवेश किया। सावधि जमा की परिपक्वता पर अल्बर्ट को कितनी राशि मिलेगी?

(A) Rs. 8600

(B) Rs. 8620

(C) Rs. 8840

(D) इनमें से कोई नहीं।

उपाय:

$$ Amount \ = Rs\left(8000× {\left(1+{5\over100}\right)^2}\right)$$

   $$ =   \left(8000×{21\over20}×{21\over20}\right)=Rs.8820 $$

Q.2. 12 p.c.p.a की दर से 3 वर्ष के बाद 25,000रु की राशि पर चक्रवृद्धि ब्याज क्या होगा?

(A) Rs. 9000.30

(B) Rs. 9720

(C) Rs. 10123.20

(D) Rs. 10483.20

(E) इनमें से कोई नहीं

उपाय:

$$ Amount \ = Rs\left(25000× {\left(1+{12\over100}\right)^3}\right)$$

  $$ =   \left(25000×{28\over25}×{28\over25}×{28\over25}\right)=Rs.35123.20 $$

∴ C.I. = Rs. ( 35123.20 – 25000) = Rs. 10123.20

Q.3 2 साल 73 दिनों के लिए प्रति वर्ष 20,480रु पर चक्रवृद्धि ब्याज, है:

(A) Rs. 2929

(B) Rs. 3000

(C) Rs. 3131

(D) Rs. 3636

उपाय:

  $$Time = 1\frac{2}{3} \ Years\ 2\frac{1}{5}Years$$

$$∴ Amount \ = Rs\left(20480× {\left(1+{25\over4×100}\right)^2}×{\left({1}+{{{1\over5}×{25\over4}}\over100}\right)}\right)$$

$$ =   \left(20480×{17\over16}×{17\over16}×{81\over80}\right)=Rs.23409. $$

∴ C.I. = Rs. (23480 -20480) = Rs. 2929.

Q.4. सैम ने एक वर्ष के लिए प्रति वर्ष 15,000रु @ 10% का निवेश किया। यदि ब्याज अर्धवार्षिक रूप से संयोजित होता है, तो सैम को वर्ष के अंत में प्राप्त होने वाली राशि होगी:

(A) Rs. 16,500

(B) Rs. 16,525.50

(C) Rs. 16,537.50

(D) Rs. 18,150

(E) इनमें से कोई नहीं

उपाय:

P = Rs. 15000; R = 10% p.a. = 5% per half – year; T = 1 year = 2 half – years.

$$∴ Amount \ = Rs\left(15000× {\left(1+{5\over100}\right)^2}\right)$$

$$=Rs{\left(15000+{21\over20}×{21\over20}\right)}= Rs.16537.50.$$

Q.5. यदि 5% प्रतिवर्ष 2 वर्षों के लिए धनराशि पर साधारण ब्याज 50रु है, तो समान दर पर और उसी समय के लिए चक्रवृद्धि ब्याज कितना है?

(A) Rs. 51.25

(B) Rs. 52.

(C) Rs. 54.25

(D)  Rs. 60

उपाय:

$$∴ Sum = \left({50×100\over2×5}\right)=Rs.500$$

    $$∴ Amount \ = Rs\left(500× {\left(1+{5\over100}\right)^2}\right)$$

  $$ =   \left(500×{21\over20}×{21\over20}\right)=Rs.551.25 $$

∴ C.I. = Rs. (551.25 - 500) = Rs. 51.25.

Q.6 4 साल के बाद 1000रु की राशि पर सरल और चक्रवृद्धि ब्याज @ 10% प्रति वर्ष के बीच क्या अंतर होगा?

(A) Rs. 31

(B) Rs. 32.10

(C) Rs. 40.40

(D) Rs. 64.10

(E) इनमें से कोई नहीं

उपाय:

$$∴ S.I = Rs.\left({1000×10×4\over100}\right)=Rs.400$$

    $$∴ C.I \ = Rs\left(1000× {\left(1+{10\over100}\right)^4}-1000\right)=Rs.464.10.$$

∴ Difference = Rs. (464.10 – 400) = Rs. 64.10

Q.7 छमाही पर सालाना 100रु पर साधारण ब्याज और चक्रवृद्धि ब्याज के बीच का अंतर 10% है:

(A) Rs. 2.50

(B) Rs. 3

(C) Rs. 3.75

(D) Rs. 4

(E) इनमें से कोई नहीं।

उपाय:

$$∴ S.I = Rs.\left({1200×10×1\over100}\right)=Rs.120$$

    $$∴ C.I \ = Rs\left(1200× {\left(1+{5\over100}\right)^2}-1200\right)=Rs.123.$$

Q.8. 30,000रु पर 7% प्रति वर्ष पर चक्रवृद्धि ब्याज 4347रु है। अवधि (वर्षों में) है:

(A) 2

(B)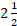

(C) 3

(D) 4

उपाय:

राशि = = Rs. (30000 + 4347) = Rs.34347.

चलो समय n साल हो। फिर,

$$3000 \left(1+{7\over100}\right)^n= 34347⟺\left({107\over100}\right)^n$$

   $$={34347\over30000}={11449\over10000}=\left({107\over100}\right)^2$$

  $$n = 2 \ Years$$

Q.9. प्रति वर्ष चक्रवृद्धि ब्याज की दर से 2 वर्ष में 1200रु की राशि 1348.32रु हो जाएगी?

(A) 6%

(B) 6.5%

(C) 7%

(D) 7.5%

उपाय:

$$1200 \left(1+{R\over100}\right)^2= 1348.32⟺\left(1+{R\over100}\right)^2$$

   $$={134832\over120000}={11236\over10000}$$

$$∴\left(1+{R\over100}\right)^2=\left({106\over100}\right)^2or \ 1+ {R\over100}={106\over100}or R=6 \% $$

Q.10 2 साल के लिए एक राशि पर चक्रवृद्धि ब्याज 832रु है और समान अवधि के लिए समान राशि पर साधारण ब्याज 800रु है। 3 साल के लिए चक्रवृद्धि ब्याज और साधारण ब्याज के बीच अंतर होगा:

(A) Rs. 48

(B) Rs. 66.56

(C) Rs. 98.56

(D) इनमें से कोई नहीं।

C.I और S.I में 2 साल के लिए अंतर = 32रु।

एक वर्ष = 400 के लिए S.I

400 रुपये पर S.I एक वर्ष के लिए = 32रु।

3 साल के लिए S.I और C.I आई में अंतर

$$= S.I = on Rs.   =   \left({832×8×1\over100}\right)=Rs. 66.56 $$

कुल अंतर = (Rs. (32+66.56) = Rs. 66.56

मुझे आशा है कि ये उदाहरण आपके लिए उपयोगी हैं। इसलिए, इन चक्रवृद्धि ब्याज समस्याओं के समाधान के साथ अभ्यास रखें और आप चक्रवृद्धि ब्याज प्रश्नों और उत्तरों का भी अभ्यास कर सकते हैं। यदि आपको समाधान के साथ चक्रवृद्धि ब्याज की समस्याओं के बारे में कोई समस्या या संदेह है, तो आप मुझसे कमेंट बॉक्स में पूछ सकते हैं।