SSC और बैंक परीक्षा के लिए उदाहरण के साथ चक्रवृद्धि ब्याज फार्मूला

छात्रों को एसएससी और बैंक परीक्षा के उदाहरणों के साथ चक्रवृद्धि ब्याज फार्मूला का सही ढंग से उपयोग करना चाहिए। क्योंकि प्रतियोगी परीक्षाओं में अक्सर चक्रवृद्धि ब्याज के प्रश्न पूछे जाते हैं। इन चक्रवृद्धि ब्याज फार्मूले का उपयोग करना मुश्किल नहीं है। आपको केवल उदाहरणों के साथ चक्रवृद्धि ब्याज के फार्मूले को सीखने या अभ्यास करने की आवश्यकता है।

तो यहां आप सीख सकते हैं या अभ्यास कर सकते हैं कि अंतर समीकरणों में चक्रवृद्धि ब्याज फार्मूला का उपयोग कैसे करें या उदाहरणों के साथ प्रश्न। आप अपने प्रदर्शन स्तर को उज्जवल करने के लिए चक्रवृद्धि ब्याज प्रश्नों और उत्तरों का भी अभ्यास कर सकते हैं।

सरल ब्याज और चक्रवृद्धि ब्याज पर समस्याओं के बारे में जानें और अपनी मानसिक क्षमता बढ़ाएं।

प्रतियोगी परीक्षाओं के लिए उदाहरण के साथ चक्रवृद्धि ब्याज फॉर्मूला

ब्याज

जब कोई व्यक्ति (उधारकर्ता) किसी दूसरे व्यक्ति या बैंक (ऋणदाता) से धन (ऋण) लेता है, तो पहला व्यक्ति किसी अन्य व्यक्ति (उधारदाता) को धन उधार के उपयोग के लिए कुछ पैसे देता है। लैंडर को भुगतान किए गए इस अतिरिक्त पैसे को ब्याज के रूप में जाना जाता है।

चक्रवृद्धि ब्याज (C.I)

गणना चक्रवृद्धि ब्याज की गणना करते समय, साधारण ब्याज जो पहले वर्ष के सिद्धांत के लिए गणना की जाती है, मूलधन में जोड़ा जाता है। इस जोड़ का परिणाम दूसरे वर्ष के लिए गणना के सिद्धांत बन जाता है और इस ब्याज को फिर से दूसरे वर्ष के लिए उपयोग किए गए सिद्धांत में जोड़ा जाता है। यह नया जोड़ तीसरे वर्ष के लिए एक प्रमुख के रूप में काम करता है और यह प्रक्रिया निर्धारित समय तक चलती रहती है। अंत में, मूल प्रिंसिपल को पिछले वर्ष की राशि से घटाया जाता है।

इस घटाव के परिणाम को चक्रवृद्धि ब्याज कहा जाता है।

महत्वपूर्ण तथ्य और सूत्र

बता दें, प्रिंसिपल = P, रेट = R% प्रति वर्ष और समय = n yr

1. यदि सालाना ब्याज मिलता है, तो

   $$ Amount\ = P \left(1+{R\over100}\right)^n $$

$$ Compound \ = P\left( {\left(1+{R\over100}\right)^n }-1\right)$$

या CI  = राशि-प्रधान

2. जब ब्याज अर्धवार्षिक रूप से संयोजित होता है:

$$ Amount\ = P \left(1+{(R/2)\over100}\right)^ {2n} $$

3. जब ब्याज त्रैमासिक होता है:

$$ Amount\ = P \left(1+{(R/4)\over100}\right)^ {4n} $$

4. जब ब्याज वार्षिक रूप से कम हो जाता है, लेकिन समय आंशिक होता है, तो  साल कहते हैं।

$$ Amount\ = P \left(1+{R\over100}\right)^ 3 × \left(1+{{2\over5}R\over100}\right) $$

5. जब दरें अलग-अलग वर्षों के लिए अलग-अलग हैं, कहते हैं, क्रमशः 1, 2 और 3 साल के लिए R1%, R2%, R3%।

$$Then, Amount = P \left(1+{R_{1}\over100}\right)\left(1+{R_{2}\over100}\right)\left(1+{R_{3}\over100}\right)$$

6. वर्तमान में n वर्ष के बराबर x मूल्य वर्तमान में दिया गया है इसलिए

 $$Present \ worth={x\over\left( 1+{R\over100}\right)^n}$$

Ex.1 2 साल के लिए प्रतिवर्ष 4% की दर से 7500रु का चक्रवृद्धि ब्याज ज्ञात कीजिए।

उपाय

$$ Amount \ = Rs\left(7500× {\left(1+{4\over100}\right)^2}\right)=Rs \left(7500× {26\over25}×{26\over25}= Rs.8112\right)$$

∴ C.I = Rs. (8112 – 7500)= Rs. 612.

Ex.2. 2 साल 4 महीने के लिए सालाना 15% पर 8000रु पर चक्रवृद्धि ब्याज ज्ञात करें, सालाना चक्रवृद्धि।

उपाय

समय = 2 years 4 month = 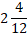  years =  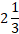years.

$$ Amount \ = Rs\left(8000× {\left(1+{15\over100}\right)^2}×{\left({1}+{{{1\over3}×15}\over100}\right)}\right)$$

  $$=Rs \left(8000× {23\over20}×{23\over20}×{21\over20} =Rs.11109.\right)$$

∴ C.I = Rs. (11109 – 8000)= Rs. 3109.

Ex.3. 10,000 रु प्रति वर्ष पर चक्रवृद्धि ब्याज 4% प्रति वर्ष की दर से पाएं, यह ब्याज अर्धवार्षिक रूप से चक्रवृद्धि है

उपाय

$$ Amount \ = Rs\left(10000× {\left(1+{2\over100}\right)^4}\right)$$

$$=Rs \left(10000× {51\over50}×{51\over50}×{51\over50}×{51\over50}\right) =Rs.10824.32.$$

C.I= Rs. (10824.32-10000)=Rs.824.32

Ex.4. 9 महीनों के लिए 20% प्रति वर्ष 20,000रु पर चक्रवृद्धि ब्याज का पता लगाएं, चक्रवृद्धि तिमाही।

उपाय

प्रिंसिपल = 16000 र; समय = 9 महीने = 3 तिमाही;

Rate = 20% per annum = 5% per quarter.

$$∴ Amount\ = Rs\left(16000 ×{\left(1+{5\over100}\right)^3 }\right)$$

  $$=\left(16000× {21\over20}×{21\over20}×{21\over20}\right)=Rs.18522$$

∴ C.I= Rs. (18522-16000)=Rs 2522.

Ex.5. यदि 3 वर्ष के लिए 5% प्रति वर्ष की दर से धनराशि पर साधारण ब्याज 1,200 रु है, तो उसी अवधि पर समान अवधि के लिए समान राशि पर चक्रवृद्धि ब्याज लगाएं।

उपाय

स्पष्ट रूप से, दर = 5% p.a, समय = 3 वर्ष, S.I = 1200रु

 $$So, Principal = \   Rs\left({100×1200\over3×5}\right) $$

   $$∴ Amount\ = Rs\left(8000 ×{\left(1+{5\over100}\right)^3 }\right)$$

  $$=\left(8000× {21\over20}×{21\over20}×{21\over20}\right)=Rs.9261$$

मुझे उम्मीद है कि उदाहरणों के साथ ये महत्वपूर्ण चक्रवृद्धि ब्याज फार्मूला आपके प्रतियोगी परीक्षाओं के लिए सहायक होगा। कंपाउंड इंटरेस्ट के सवालों का हिंदी में अभ्यास करें और प्रतियोगी परीक्षा में बेहतर रैंक प्राप्त करें।

यदि आप किसी भी समस्या या संदेह है तो उदाहरण के साथ टिप्पणी अनुभाग में कुछ भी संबंधित चक्रवृद्धि ब्याज फार्मूला में मुझसे पूछें।