SSC और बैंक परीक्षाओं के समाधान के साथ चेन रुल की समस्याएं

हर सवाल का हल होता है। कुछ छात्रों ने समाधान ढूंढ लिया है और कुछ को समाधान नहीं मिल रहा है। वैसे ही जैसे चेन रूल की समस्याओं का समाधान होता है लेकिन कुछ छात्रों को चेन रूल की समस्याओं को हल करने में कठिनाई का सामना करना पड़ता है। तो, यहां आप आसानी से सीख सकते हैं कि SSC और बैंक परीक्षाओं के समाधान के साथ चेन रुल की समस्याओं को कैसे हल किया जाए।

आप इन चेन रूल प्रॉब्लम्स विद सॉल्यूशंस की मदद से प्रतियोगी परीक्षाओं में सफलता की संभावना बढ़ा सकते हैं क्योंकि प्रतियोगी परीक्षाओं में पूछे जाने वाले समान प्रश्न यहाँ के उदाहरण के रूप में हैं।

आप अपनी सीखने की प्रक्रिया को पूरा करने के बाद चेन रुल के प्रश्नों और उत्तरों का भी अभ्यास कर सकते हैं।

प्रतियोगी परीक्षाओं के समाधान के साथ चेन रुल की समस्याएं

Q.1. यदि 15 खिलौनों की कीमत रु. 234, 35 खिलौनों की कीमत क्या है?

समाधान:

मान लीजिए कि आवश्यक लागत रु. x फिर,

अधिक खिलौने, अधिक लागत              (सीधा अनुपात)

∴ 15 : 35 :: 234 : x ↔ (15 × x) = (35 × 234)  $$   ↔\ x =  \left({35×234\over15}\right)= 546 $$

अत: 35 खिलौनों का मूल्य 546 रुपये है

Q.2. यदि 15 दिनों के लिए 6 पुरुषों की मजदूरी 2100रु हो, तो 9 पुरुषों की 12 दिनों की मजदूरी पाएं।

समाधान:

माना आवश्यक मजदूरी xरु है।

अधिक पुरुष, अधिक मजदूरी          (सीधा अनुपात)

कम दिन, कम मजदूरी            (सीधा अनुपात)

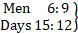 : : 2100 : x

∴ (6 × 15 × x ) = (9 × 12 × 2100) $$  ↔\ x =   \left({9×12×2100\over6×15}\right)= 2520 $$

अत: अभीष्ट मजदूरी 2520रु है।

Q.3. यदि 15 पुरुष, 9 घंटे प्रतिदिन कार्य करते हुए, 16 दिनों में एक खेत की कटाई कर सकते हैं, तो 18 व्यक्ति प्रतिदिन 8 घंटे कार्य करते हुए खेत की कटाई कितने दिनों में करेंगे?

समाधान:

माना दिनों की अभीष्ट संख्या x है।

अधिक पुरुष, कम दिन                       (अप्रत्यक्ष अनुपात)

प्रति दिन कम घंटे, अधिक दिन      (अप्रत्यक्ष अनुपात)

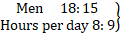 :: 16 : x

∴ ( 18 × 8 × x) = ( 15 × 9 × 16) $$  ↔\ x =  \left({15×144\over144}\right)= 15 $$

अत: अभीष्ट दिनों की संख्या = 15.

Q.4. यदि 6 खिलौनों का मूल्य रु. 264.37, 5 खिलौनों की अनुमानित कीमत क्या होगी?

समाधान:

मान लीजिए कि अभीष्ट मूल्य रु. x। फिर, कम खिलौने, कम लागत (प्रत्यक्ष अनुपात)

∴ 6 : 5 : : 264.34 : x ↔ ( 5 × 264.37) $$  ↔\ x =   \left({5×264.37\over6}\right)x= 220.308 $$

∴ 5 खिलौनों की अनुमानित कीमत= Rs. 220

Q.5. एक किले में 150 आदमियों के लिए 45 दिनों तक भोजन की व्यवस्था थी। 10 दिनों के बाद, 25 लोगों ने किले को छोड़ दिया। शेष भोजन कितने दिनों तक चलेगा?

समाधान:

10 दिनों के बाद : 150 पुरुषों ने 35 दिनों तक भोजन किया।

मान लीजिए 125 पुरुषों ने x दिनों के लिए भोजन किया। अब, कम पुरुष, अधिक दिन (अप्रत्यक्ष अनुपात)

∴ 125 : 150 : : 35 : x ↔ 125 ×  x = 150 × 35  $$  ↔\ x =  \left({150×35\over125}\right)x= 42 $$

इसलिए बचा हुआ खाना 42 दिनों तक चलेगा।

Q.6. यदि 36 पुरुष किसी कार्य को 25 घंटे में कर सकते हैं, तो 15 पुरुष उस कार्य को कितने घंटे में करेंगे?

समाधान:

माना घंटों की आवश्यक संख्या x है। फिर,

कम पुरुष, अधिक घंटे       (अप्रत्यक्ष अनुपात)

∴ 15 : 36 : : 25 : x ↔ (15 × x) = ( 36 x 25)  $$  ↔\ x =  \left({36×25\over100}\right)= 60 $$

Q.7. यदि 20 आदमी 56 मीटर लंबी दीवार को 6 दिनों में बना सकते हैं, तो 35 आदमी 3 दिनों में कितनी लंबाई की दीवार बना सकते हैं?

समाधान:

माना दिनों की आवश्यक संख्या x मीटर है

अधिक पुरुष, अधिक लंबाई निर्मित                   (सीधा अनुपात)

कम दिन, कम लंबाई का निर्माण                        (सीधा अनुपात)

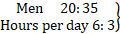: : 56 : x

∴ ( 20 × 6 × x ) = ( 35 × 3 × 56) $$  ↔\ x =   \left({35×3×56\over120}\right)= 49 $$

अतः अभीष्ट लम्बाई 49 m है।

Q.8.  यदि x मीटर तार का मूल्य d रुपये है, तो उसी दर पर y मीटर तार का मूल्य क्या है?

समाधान:

x मीटर की लागत = रु.डी. 1 मीटर की लागत = Rs. $$   =   Rs\left({d\over x}\right) $$

Cost of y meters   $$    =  Rs\left({d\over x}×y\right)=  Rs\left({yd\over x}\right) $$

Q.9. 36 पुरुष एक कार्य को 18 दिनों में पूरा कर सकते हैं। 27 आदमी उसी काम को और कितने दिनों में पूरा करेंगे?

समाधान:

माना दिनों की अभीष्ट संख्या x है।

फिर, कम पुरुष, अधिक दिन (अप्रत्यक्ष अनुपात)

∴ 27 : 36 :: 18 : x ↔ 27 × x. ↔ 27 ×  x = 36 × 18  $$   ↔\ x =   \left({36×18\over27}\right)x= 24 $$

Q.10. एक पहिया जिसमें 6 कोग होते हैं, उसे 14 कॉग के बड़े पहिये के साथ जोड़ा जाता है। जब छोटे पहिये ने 21 चक्कर लगाए हैं, तो बड़े पहिये द्वारा किए गए चक्करों की संख्या है:

समाधान:

माना बड़े पहिये द्वारा किए गए परिक्रमण की आवश्यक संख्या x है।

फिर, अधिक कोग, कम क्रांति (अप्रत्यक्ष अनुपात)

∴ 14 : 6 : : 21 : x ↔ 14 ×  x = 6 × 21 $$  ↔\ x =   \left({6×21\over14}\right)= 9. $$

इन 10 समाधानों की सहायता से, आप चैन रुल की समस्याओं को हल करने के लिए एक विचार ले सकते हैं जो आपकी प्रतियोगी परीक्षाओं में आपकी सहायता करेगा। यदि आप समाधान के साथ चैन रुल की समस्याओं के बारे में कोई संदेह रखते हैं तो आप मुझसे कमेंट बॉक्स में पूछ सकते हैं।