

फॉर्मूला, प्रश्नों को जल्दी हल करने में मदद करता है लेकिन आपको केवल यह सीखने की आवश्यकता है कि समस्या को हल करने के लिए किसी भी सूत्र का उपयोग कैसे किया जाए। आज मैं फॉर्मूला के उपयोग को समझने के लिए महत्वपूर्ण सरल ब्याज फॉर्मूला उदाहरण सहित दे रहा हूँ। समस्याओं को शीघ्रता से हल करने के लिए इन सरल ब्याज सूत्रों को याद रखें और उदाहरणों के साथ सरल ब्याज फॉर्मूला सीखें।
सरलब्याज क्वानटेटिव एप्टीट्यूड का एक महत्वपूर्ण टॉपिक है। हर साल एसएससी, बैंक और अन्य प्रतियोगी परीक्षा में सरल ब्याज के 2-3% प्रश्न पूछे जाते हैं। सरल ब्याज के फार्मूले का उपयोग सीखने के बाद आप उत्तर के साथ सरल ब्याज के प्रश्नों का अभ्यास कर सकते हैं।
सरल ब्याज की परिभाषा: यदि किसी विशेष अवधि/समय के लिए उधार ली गई राशि पर ब्याज की गणना समान रूप से की जाती है तो इसे सरल ब्याज कहा जाता है।
प्रिंसिपल परिभाषा: एक निश्चित अवधि/समय के लिए उधार/उधार लिया गया धन प्रिंसिपल/योग कहलाता है।
ब्याज की परिभाषा: दूसरे के पैसे का उपयोग करने के लिए भुगतान की गई अतिरिक्त राशि को ब्याज कहा जाता है।
प्रिंसिपल = P
दर = R% प्रति वर्ष (p.a)
समय = T वर्ष
राशि = A
(1) सरल ब्याज फॉर्मूला:
S.I = 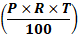
(2) प्रिंसिपल के लिए फॉर्मूला:
P = 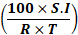
(3) ब्याज दर के लिए फॉर्मूला:
R = 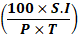
(4) समय के लिए फॉर्मूला:
T = 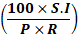
(5) शुद्ध राशि के लिए फॉर्मूला
A = P+I
प्र.168,000 पर
समाधान:
P= Rs. 68000, R=
S.I =
=Rs. 8500
प्र.2 4 फरवरी, 2015 से 18 अप्रैल 2015 तक की अवधि के लिए 3000रु पर
समाधान:
समय = (24+31+18) days = 73 days =
P = Rs. 3000 और R =
S.I = Rs.
= Rs. 3750
Q.3 यदि कोई धनराशि सरल ब्याज पर 'T' वर्ष में 'n' गुना हो जाती है, तो ब्याज की गणना का सूत्र R =
उदा. सरल ब्याज पर एक राशि 20 वर्षों में चार गुना हो जाती है। ब्याज दर ज्ञात कीजिए।
समाधान:
यहां, T = 20 yers, n= 4p
R=
= 15
मुझे उम्मीद है कि उदाहरण के साथ दिया गया यह सरल ब्याज फॉर्मूला आपको प्रतियोगी परीक्षाओं में सरल ब्याज की समस्याओं को जल्दी और सही तरीके से हल करने में मदद करता है। उत्तर के साथ अधिक सरल ब्याज वाले प्रश्नों का अभ्यास करें।
अधिक सरल ब्याज प्रश्नों और उत्तरों के लिए, अगले पेज पर जाएँ।
Examsbook Prep ऐप आज ही प्राप्त करें